缘由
看ADC测试,在量化噪声那一块儿遇到了一个问题-输入正弦波时,为什么可以把输入信号看作均匀分布的?
之前写出来pdf,是一个bathtube,我认为可以近似地看成均匀的,只有两侧比较不均匀。但看ADI-MT001中对这个问题似乎有所说明,在一篇上个世纪的文章中提到过,那就不妨看看实际推导。
部分译文
语音信号的幅度量化是最近的一项创新。这里我们不允许从连续的幅度域中选取,而是从确定的离散值中选取。这意味着,原始的语音信号会被从可用的离散集合中亿最小误差基础选择的固定值重建的波形取代。显然如果我们让量化值之间的间隔足够近,可以让量化后的波形和原始信号用耳朵分辨不出。幅度量化的目的是,抑制传输介质中的干扰影响。通过使用精密的接收仪器,我们能够恢复接收到的值,而不会受到叠加干扰的任何影响,只要干扰不超过相邻步长的一半。
通过幅度和时间上量化的结合,我们可以为语音信号编码,因为现在的传输能够在每个离散时间间隔内发送离散的幅度。通过使用二进制表示每个离散的信号幅度,其中只有0和1被使用,这个方法获得了克服干扰的最大优势。十进制中的4在二进制中表示为100,8是1000,16是10000,等等。通常情况下,如果我们在二进制系统中有N位数字位,那么我们可以构建$2^N$个不同的数字。如果需要的离散幅度不超过$2^N$个,那么在每个采样间隔内,可以通过N个开关脉冲的序列来发送完整的信息…
为了确定用来传输语音信号需要的量化步长数量,我们需要知道失真和步长之间的关系。这正是本文的主题。我们把这个问题分为两部分:仅仅是幅度上的量化;时间量化和幅度量化的结合。前者可以使用简单的“阶梯转换器”处理,是有着图1中输入输出曲线的设备。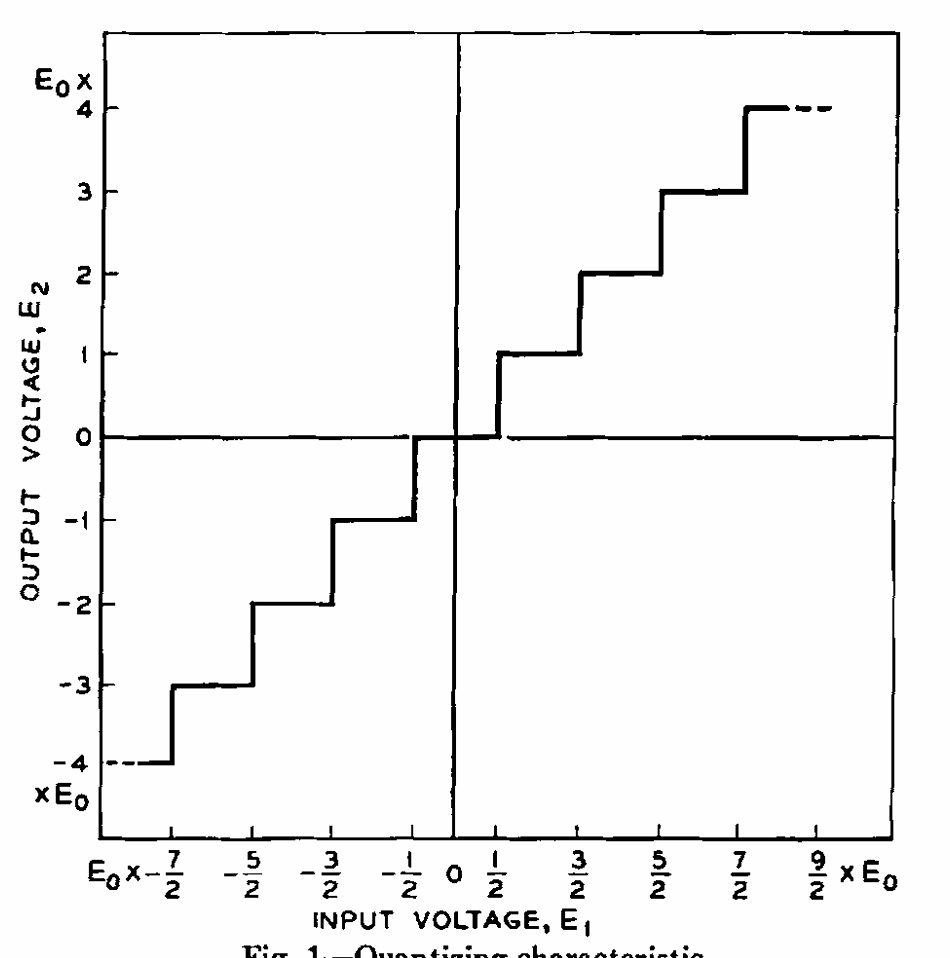
阶梯转换器上的信号被分为不同的电压切片,所有的在切片中止的正负一半步长以内的信号,都被这个中值所替代。当输入是一个光滑变化的时间函数时,对应输出是图2中的样子: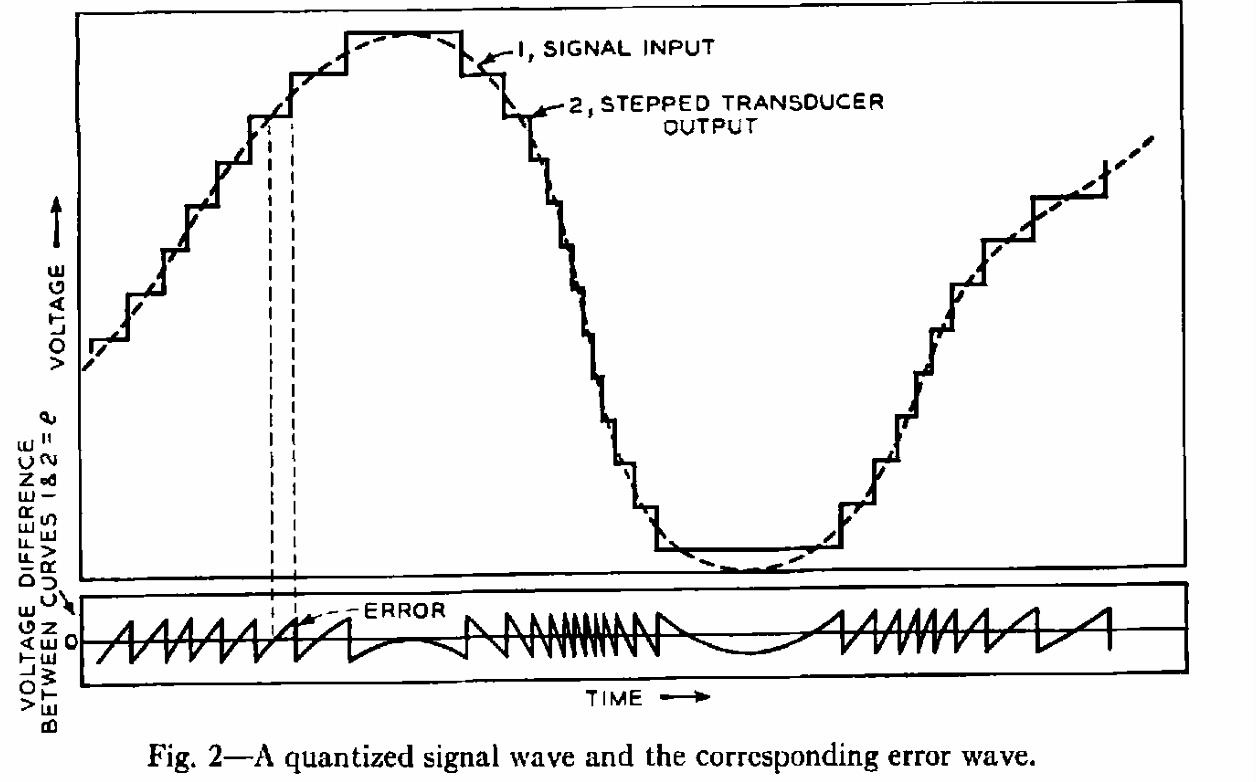
如果有大量的小步长,那么误差信号类似于一系列斜率不同的直线,但几乎一直在正负一半步长的间隔内延申。紧密的相隔步长的极限情况,让我们能够相当简单地推导出均方误差意义上相当接近的值,稍后将会证明在大多数相当重要的情形下是足够精准的。如果$E_0$是一个步长,s是斜率,那么典型的误差线表示为:
$$\epsilon=st,-\frac{E_0}{2s}<t<\frac{E_0}{2s}$$
这里$\epsilon$是误差,t是相对于中点的时间,那么均方误差就是:
$$\epsilon^2=\frac{E_0^2}{12}$$
积分过程略去。
并不是所有的失真都落在信号频带里面。失真可能是非线性特性带来的。高阶调制得到的结果可以通过滤波除去。因此,计算误差波形的频谱就十分重要了。下一个部分我们将会进行