1.量化噪声带来的谐波

之前看ADC测试时，两本书中都强调了一个表达式：
$$\frac{f_{in}}{f_s}=\frac{M}{N}$$
其中M必须是素数，否则在输出中会有重复的图样。

如果做个纠正，应该满足：M与N互素。这个条件使得FFT输入序列不是周期的。关于这个问题的透彻理解实际上来自这篇文章：DSP-Based Testing – Fundamentals 7 Coherent Condition

对“重复图案”这点，我其实是理解的。如果FFT输入序列是周期的，量化噪声就是周期的，丧失了随机性，得到的结果也就是不准确的。

但是关于“谐波”，我之前一直不理解。上过的信号课程告诉我，只要相干采样就不会有什么问题。我自己拿matlab写了个FFT程序仿了一下，也没问题，输出是一根干净的谱线，连噪底都没有。

但这样实际上是忽略了量化噪声。如果在仿真生成FFT输入数据的时候取个整，或许就能得到符合实际的结果。

量化噪声也是周期的。 这句话是问题关键所在。对应频率以及谐波处就会有谱线。下面简单写个matlab程序跑一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
%% quantization error periodic
clear;
close all;
clc;

%% 
f_s  = 512;%sampling frequency
f_in = 64;%input frequency

n = 0:511;

T = 1/f_s;
t = n * T;


y = round(sin(2*pi*f_in*t));

Y = abs(fft(y));

subplot(1,2,1);

stem(t(1:64),y(1:64));
xlabel("t");
ylabel("Magnitude");
title("Sampled Data");
grid on;% Time Domain


subplot(1,2,2);
plot(0:255,Y(1:256));

xlabel("$f/Hz$");
ylabel("Magnitude");
title("FFT");
grid on;%Freq Domain

下面是运行结果：
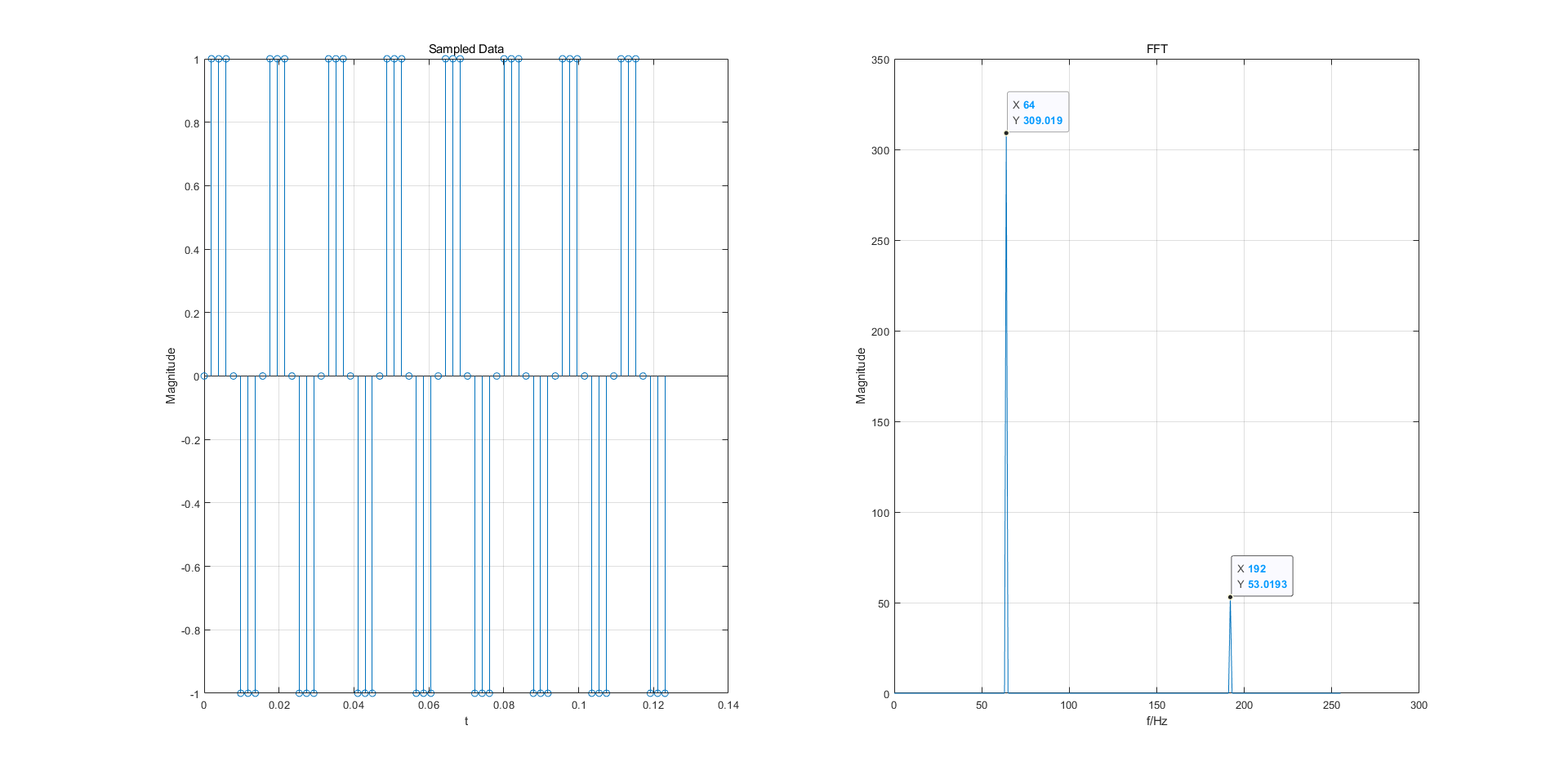
error

可以看到有一个三次谐波。

2.关于ENOB公式

我们熟知的ENOB公式是：

$$ENOB=\frac{SINAD-1.76dB}{6.02dB}$$

但ADI handbook以及IEEE standard中给出了另一个计算ENOB的式子：

$$ENOB=N-log_2[\frac{Q_A}{Q_T}]$$

其中$Q_T$是量化噪声，$Q_A$是实际噪声的均方根值。

为什么会有这样的结果？究竟是不同的定义，还是另有原因？

其实，新的式子只是我们熟知的式子的近似。

熟知的公式：$ENOB = \frac{SNR-1.76}{6.02}$

理论上的SNR：$SNR=20lg\frac{A_S}{Q_T}$

实际上的SNR：$SNR=20lg\frac{A_S}{Q_A+Q_T}$

SNR差值：$\Delta SNR = 20lg\frac{Q_A+Q_T}{Q_T}$

则实际的ENOB：$ENOB=\frac{SNR-1.76-\Delta SNR}{6.02}$

把$\Delta$项提出来，$\Delta SNR/6.02 = \Delta/20lg2 = \frac{lg\frac{Q_A+Q_T}{Q_T}}{lg2}$，又：实际的ADC中$Q_A \gg Q_T$，可以化简为：$\frac{lg\frac{Q_A}{Q_T}}{lg2}=log_2\frac{Q_A}{Q_T}$

则$ENOB=N-log_2\frac{Q_A}{Q_T}$

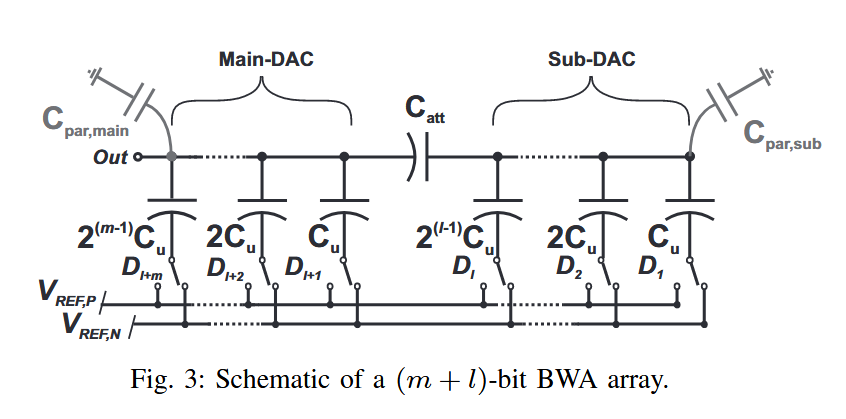
3.关于分段电容结构的CDAC

bwa-cdac