动态ADC测试
目前绝大多数(The vast majority of)集成电路ADC都是包含一种或另一种内部采样保持功能的采样ADC。除了传统的直流规格,采样ADC通常在交流性能方面被规定,比如SINAD,ENOB,SNR,SFDR,等等。在二十世纪七十年代早期,绝大部分交流测试都是使用“背对背”测试方法进行的,会使用一个高性能DAC来重建ADC的输出,因此允许使用传统的模拟测试装置。在二十世纪七十年代中期,以数字信号处理为基础的(DSP-based)ADC测试方法开始演变–今天,几乎(practically)所有的ADC测试都是对ADC的输出数据进行某种数字分析。尽管生产商提供的评估板,以及以计算机为基础的软件包,让数字技术可以被大部分严肃的ADC使用者获取到,但对一些旧的方法的考察还是一些有意义的工作。
在这一部分,我们将会讨论一些传统的“背对背”测试方法,它们在今天的台架测试装置中依然有应用;同时也会介绍更新的DSP-based方法。在适用的情况下,还讨论了关于信号发生的话题。
手动“背对背”动态ADC测试
图5.44展示了一个典型的“背对背”ADC交流测试装置。和在静态测试中使用这个方法一样,成功的关键是找到一个至少比待测ADC有着至少2-bit以上的直流和交流性能的DAC。在二十世纪七十到八十年代,这不是什么大问题,因为12-bit快稳定、相对低失真的DAC是寻常可见的–有时需要使用外部的deglitcher(glitch是毛刺)来获得相对低水平的失真。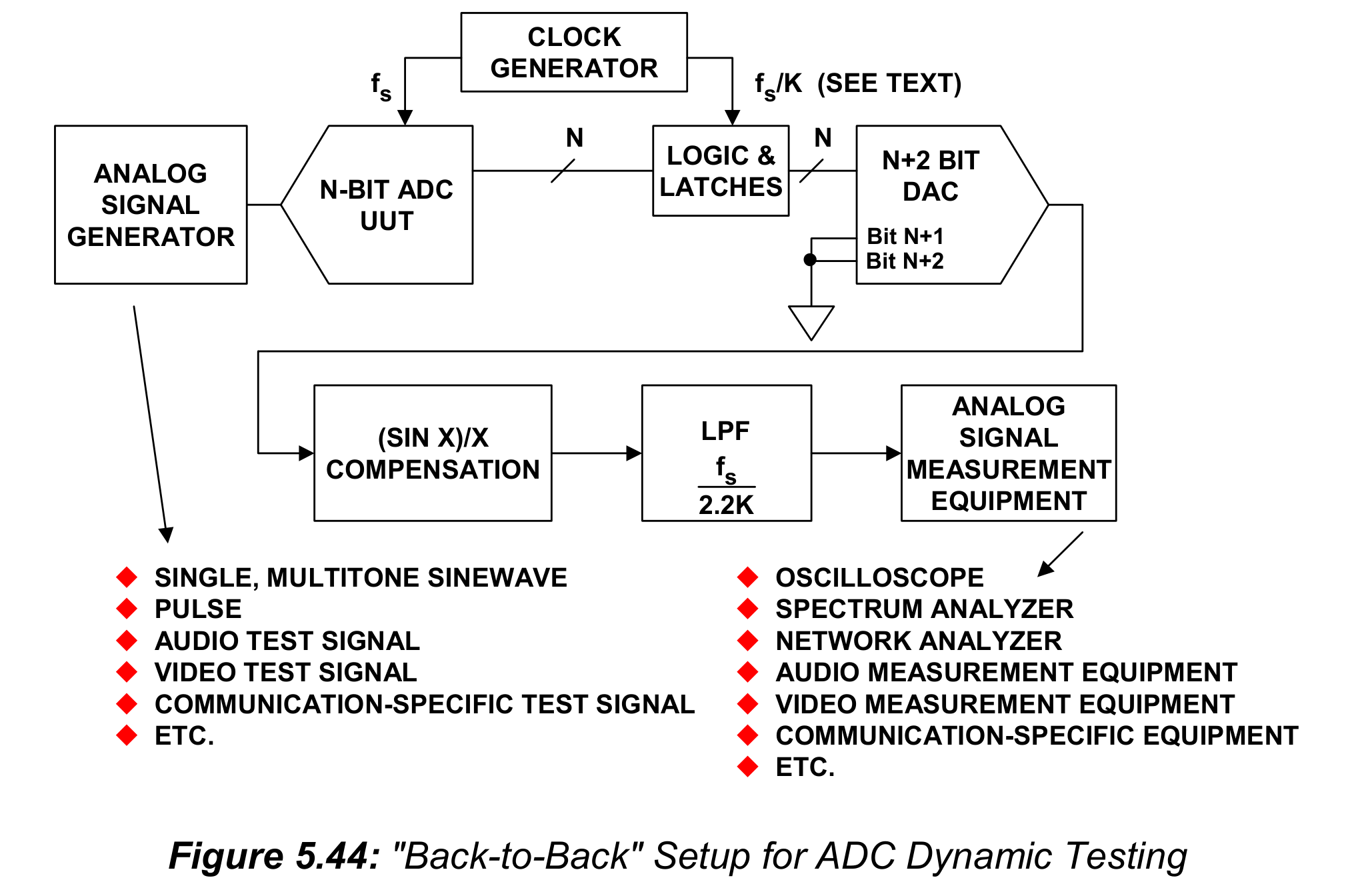
背对背方法被广泛应用于8和10-bit高速ADC中。在此期间大部分生产商的ADC评估板都半酣一个重建DAC,大部分情况下是足够用来做一下基本的交流测试的。但在今天,如果ADC评估板中包含一个重建DAC,它通常是为了方便实现一些简单的功能测试–实际的交流评估还需要使用DSP技术来做。
在今天,背对背测试仍然适用于将信号数字化、处理再转换回模拟形式的应用中,例如音频编码。在这种情形,ADC/DAC结合后的背对背表现能决定整个系统的性能,并且精确地知道交流误差是怎么在ADC和DAC之间分配是不重要的。在这些应用中,可以使用前面描述的测量SNR/SINAD/THD/SFDR的模拟测试方法。
今天,有许多高性能高速ADC,对它们而言挑选适合测试的交流兼容的DAC是很困难的。通信应用中的12-,14-和16-bit分辨率的ADC尤其如此。在很多情形中,最匹配的是有着完整交流规格的适用于DDS应用的DAC,比如TxDAC®系列。
TxDAC®:ADI的一个产品系列
回到图5.44来,重建DAC的输出是一串矩形波,时宽等于采样频率的倒数(reciprocal)。如本书第二章中讨论的那样,信号的频率响应遵循$(sinx)/x$函数,因此依赖于频率效应的系统测量必须考虑理论滚降,或者包含一个合适的补偿滤波器。
补充说明:
尽管没看这本书的第二章,但Data Converters第二章也讲了这一部分。重建信号的频谱等于采样后冲激串的频谱(也就是原始模拟信号周期延拓)乘$(sinx)/x$。
在许多情况下,把重建DAC的时钟设置为ADC采样频率的偶数K分之一(也就是采样频率是时钟频率的偶数倍)是很有用的,比如K=2、4、8倍,能够缓解DAC所需的建立时间。输出低通滤波器被选择为截止频率大约在$f_s/2.2K$,以至于在感兴趣的频带外频谱能够衰减。
如同之前提到的那样,“背对背”测试的一个优点是,可以使用与传统应用相关的模拟测试装置(像图5.44中列出的那样),而不需要额外的硬件或者DSP-based软件。
使用背对背测试装置进行交流线性度测试,最强大的两个测试是包络测试和拍频测试。包络测试使用接近$f_s/2$的信号来测量ADC交流性能,而拍频测试使用的信号接近$f_s$–两个测试使用了相同的测试装置,像图5.45中展示的那样。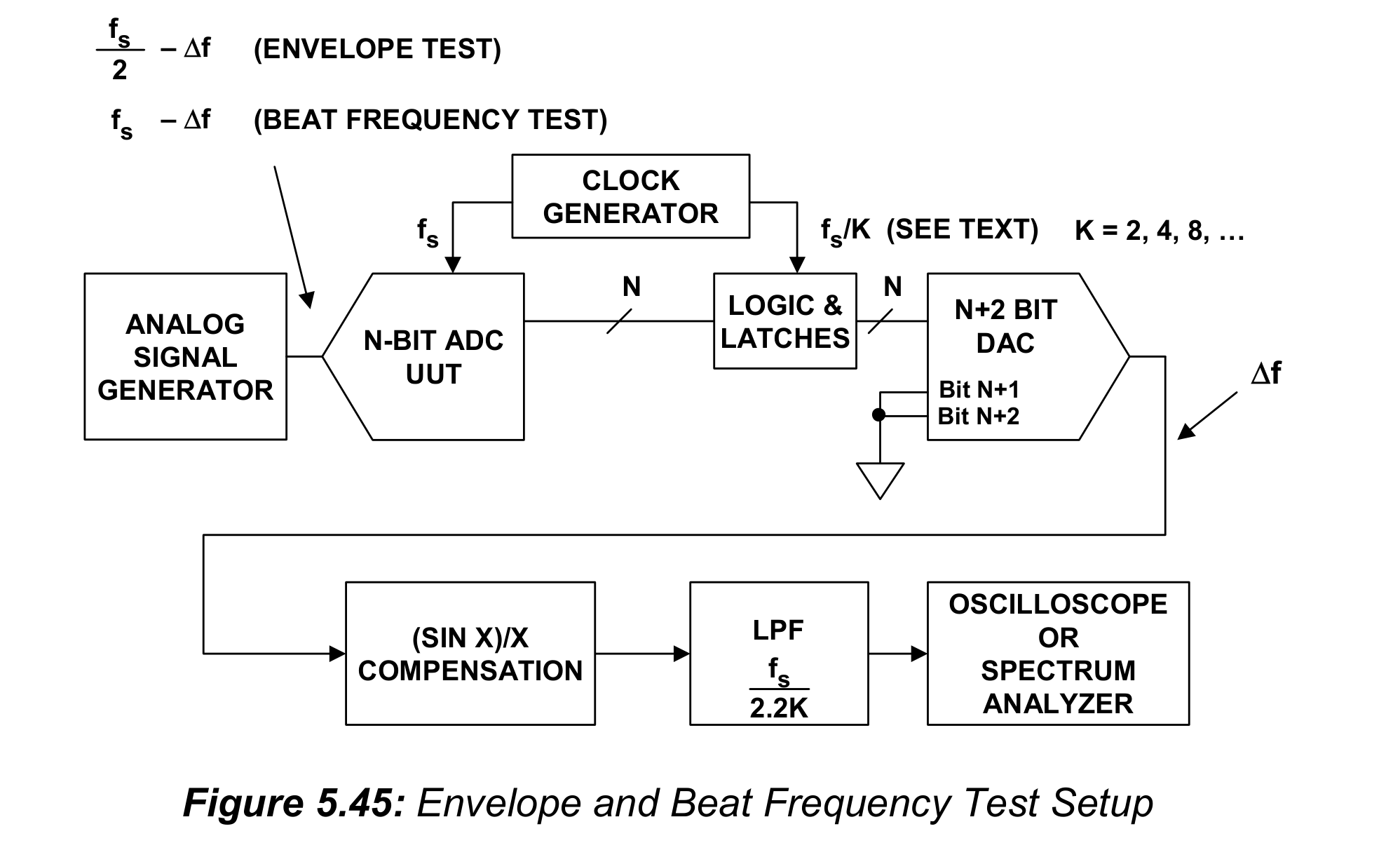
图5.46中展示了包络测试中的采样信号,在这里输入信号频率是$f_s/2$稍微低了$\Delta f$后的结果。注意到低频的$\Delta f$信号会出现在两个包络中。如果把DAC的时钟设为ADC时钟的一半,也就是K=2,那么每个ADC其他样本都被时钟送进重建DAC中,产生低频$\Delta f$信号,去除其中一个包络。在实际中,这样能够减少DAC稳定时间故障的影响,并且低频$\Delta f$信号能够轻松地通过示波器来观察非线性度和失码,或者通过频谱分析仪来测量失真。几百kHz的$\Delta f$通常能满足要求。采样时钟和输入信号都应该来自于稳定的频率合成器或晶振,来防止低频信号上的相位噪声。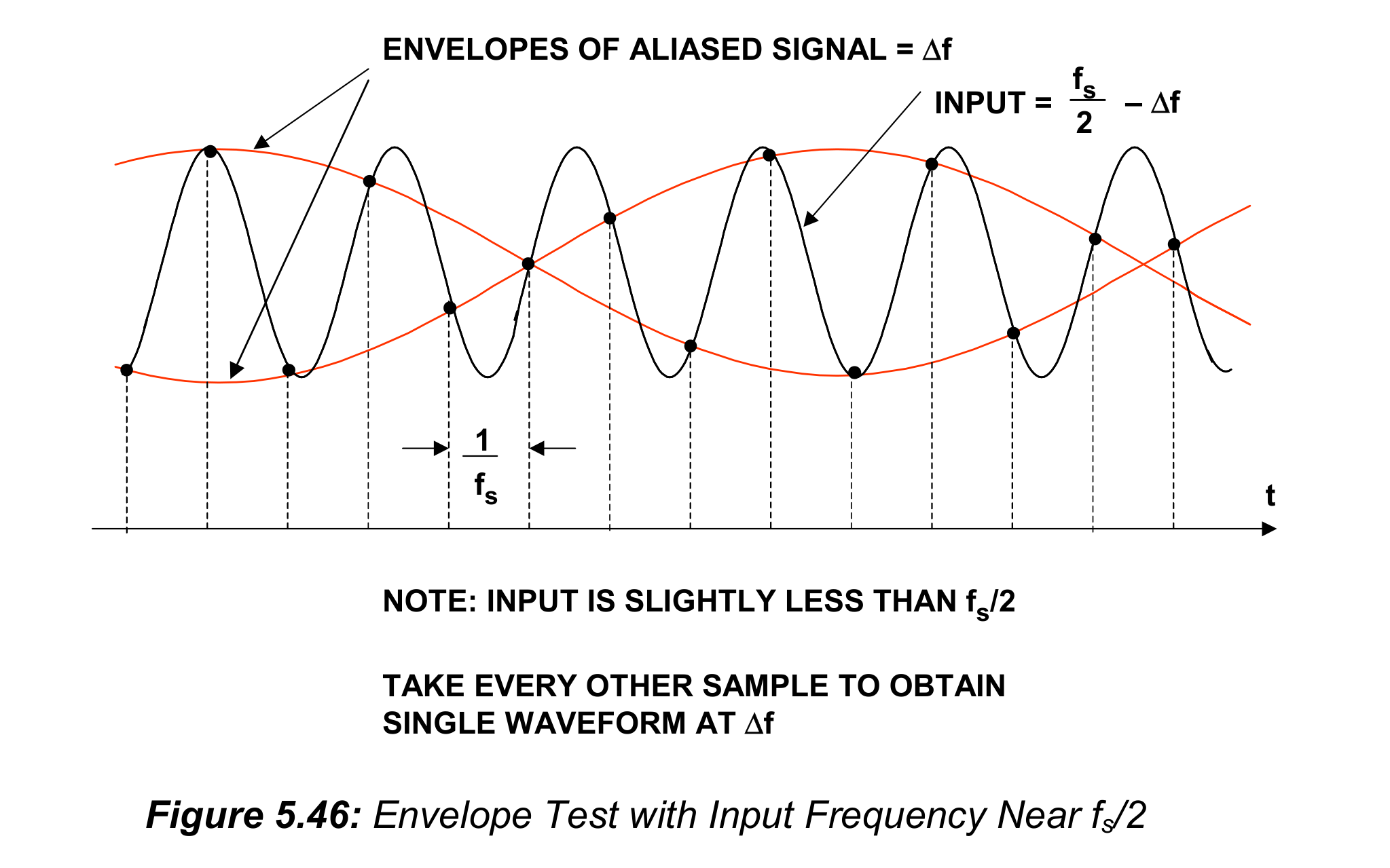
关于包络测试:
这里将K设定为2,那么重建频率相当于$f_s/2$,用它来重建$f_s/2-\Delta f$的信号,信号频率自然是$\Delta f$。
而拍频测试基本上(essentially)与包络测试相同,除了输入信号放在接近采样频率$f_s$的位置,如图5.48所示。这种情况下,不需要将采样时钟进行分频,直接把时钟输入给DAC(也就是K=1),就能得到低频的“拍”信号。但是,如果将采样频率分频后再送给DAC,能够降低对稳定时间故障的敏感性,如同包络测试中那样。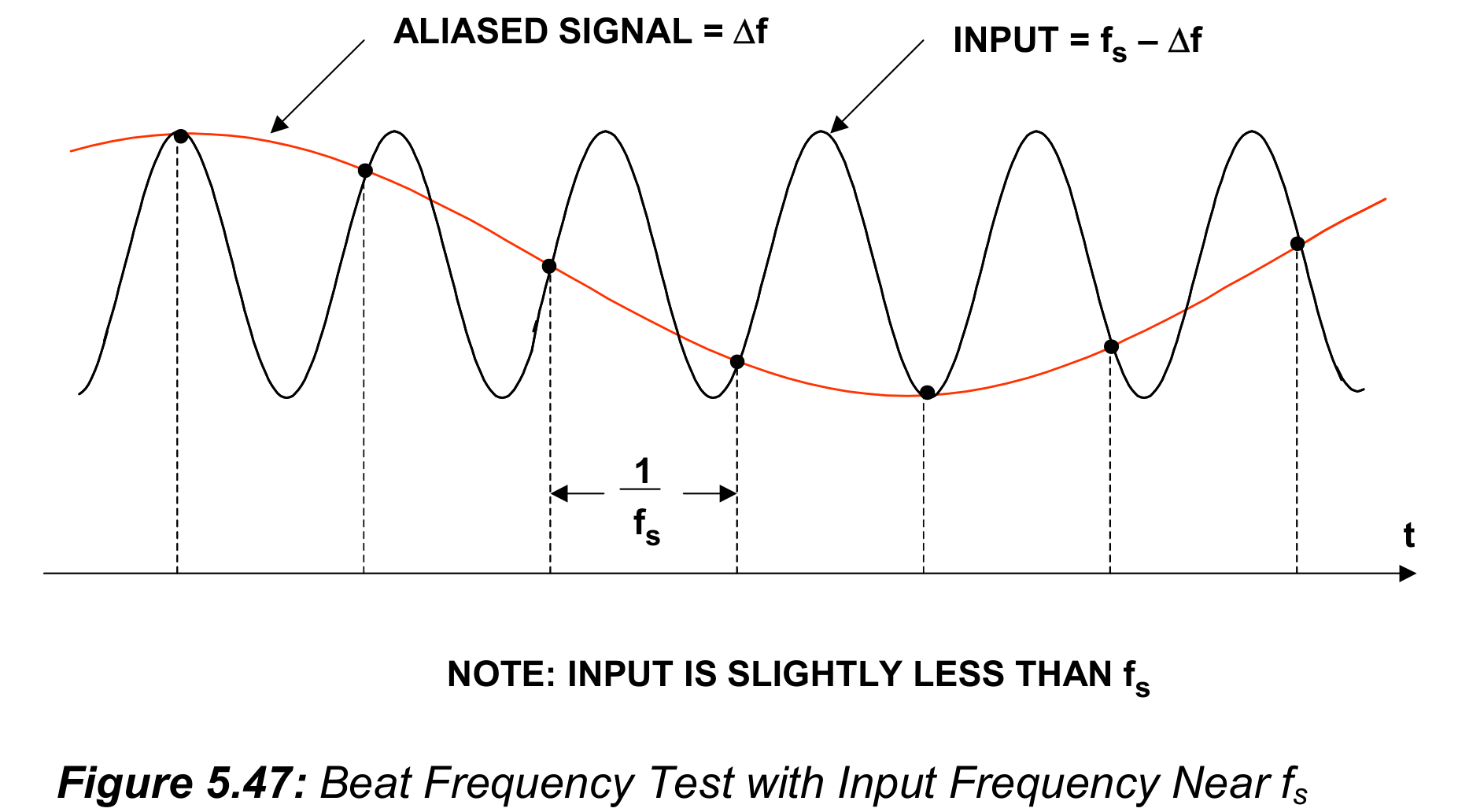
应当指出的是,如果DAC分频设置为K=2,则可以在接近$f_s/2$的任意倍数处观察到低频的$\Delta f$信号,因此允许ADC用于欠采样应用中的评估。因子K应该至少为2,来消除接近$f_s/2$倍数处的双包络。如果DAC需要更多的稳定时间来产生一个低频信号的清晰显示,K可以被选为4或者8.
大体的(gross)交流非线性和失码可以使用示波器观察,如图5.48中展示的那样。图中的测试是由8-bit flash ADC在20MSPS采样率进行的,输入信号微微偏移。右侧的expanded view展示了flash ADC中匹配不足的影响。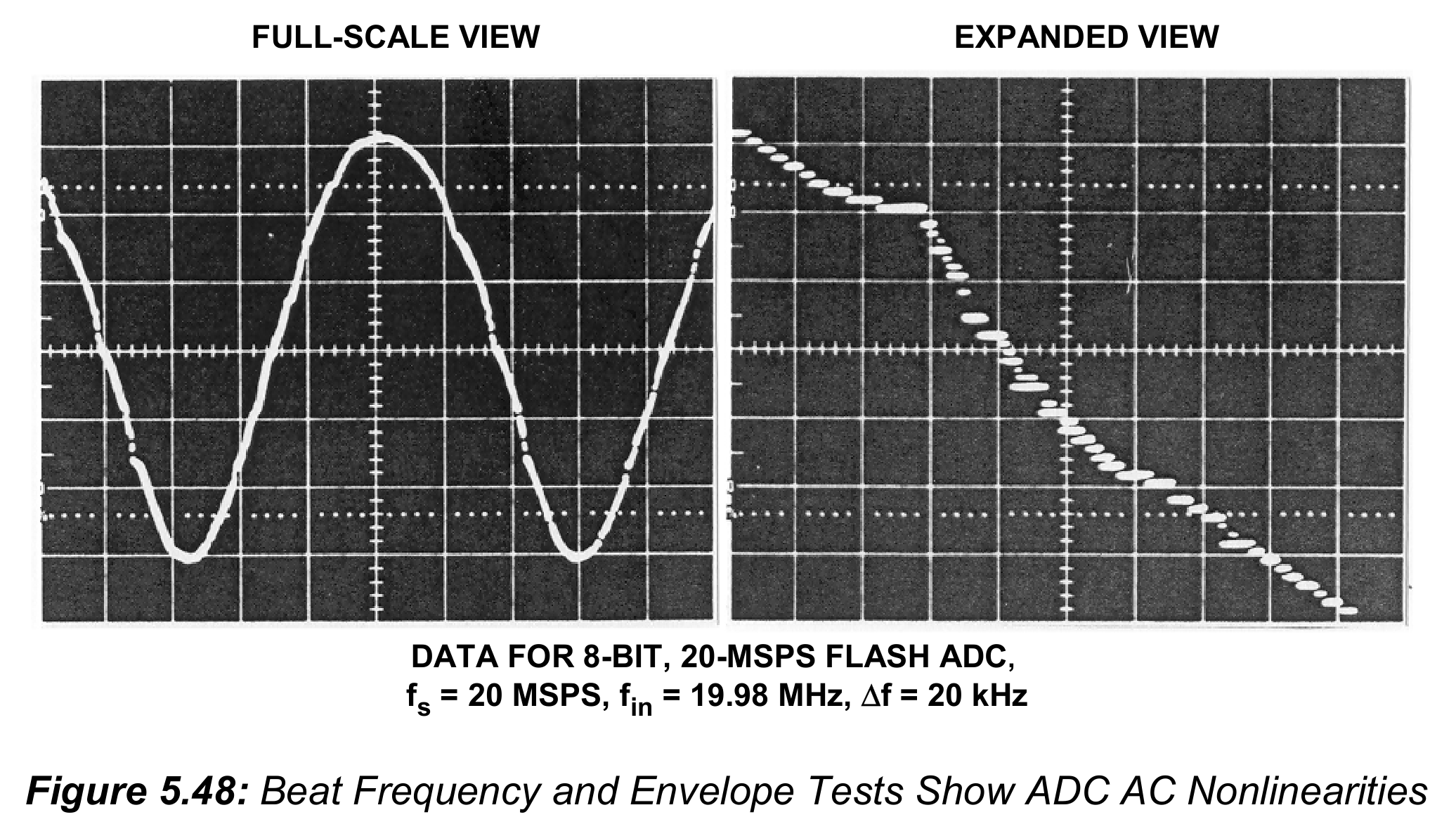
最后,背对背测试装置可以用来简单地测量ADC的大信号输入带宽。对这个测试,在补偿、滤波和同步到采样时钟之前,一个示波器直接连接到DAC输出。输入正弦波被设定在低频率并调整,直到DAC指示ADC几乎没有消除输入信号的正负峰值。然后可以增加输入频率,然后重复测试。为了造成削波而增加的输入信号电平对应着ADC增益的下降;而输入电平的下降暗示着增益的上升。这个测试可以扩展到奈奎斯特频率,因为DAC响应并不关键–它只是被用来探测ADC的削波点。小信号带宽也可以被测量,其中输入正弦波被设定为在每个测试频率能够激活相同地的预设数目的DAC电平(也就是规定好需要激活的DAC电平数目,在每个频率都调整输入正弦波来达到这个数目,比较不同频率输入正弦波的电平)。
总而言之,背对背ADC测试方法可以充当一个ADC整体交流性能的快速检查,这是对于分辨率高达10-bit的ADC而言。在将重建DAC与ADC结合的系统中,它也可以用来测试端到端性能。高性能ADC,12-bit或者更高分辨率,它们的严格评估需要数字技术的使用,会在接下来几个部分中讨论。对这种(高性能)ADC,背对背测试也是有用的,但只能用于功能的快速检查。
使用正弦波曲线拟合测量有效位数(ENOB)
第一个要讨论的DSP-based测试时使用正弦波曲线拟合测试ENOB。为了(in order for)使结果有效,输入频率一定不能是采样频率的子谐波。这个需要在本书第二章中已经讨论过,本章DAC测试部分也讨论过。M个样本(数据记录长度)被采集到缓存中。一个很好的经验法则是,使M足够大以至于能够包含输入正弦波的至少五个周期。然后这些数据被读入电脑中,然后计算出一个最佳拟合正弦波。使用最佳拟合正弦波与实际样本点的均方根误差来计算ENOB。将驱动内存的时钟频率降到$f_s/K$可以环节对缓存的要求,代价是测试时间会上升。图5.49展示了测试装置。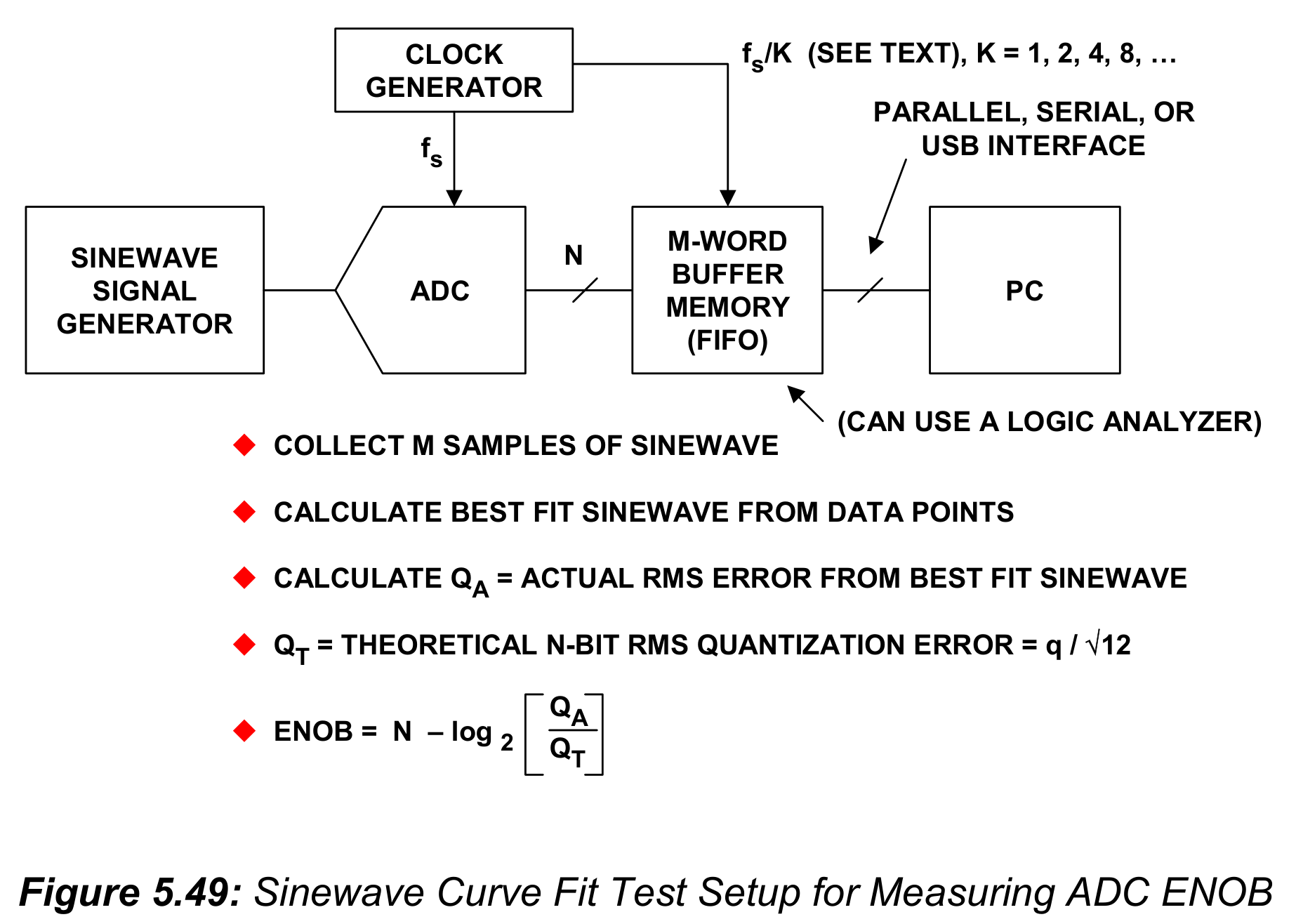
算法必须计算幅度、相位、频率,以及最佳拟合曲线的偏差(4参数)。有许多可用的算法,在参考文献中有提到。如果输入频率和采样率精确已知,需要使用3参数算法(4参数算法未必收敛)。一旦知道了最佳拟合正弦波,实际的均方根量化误差,$Q_A$,就能通过数据记录中的点来记录出。这个值包括由INL,DNL,失码,孔径抖动,噪声等因素带来的误差。理论均方根误差,众所周知,是$Q_T=q/\sqrt{12}$,这里q是LSB的权重。有效位数(ENOB)可以通过下式计算:
$$ENOB=N-log_2 [\frac{Q_A}{Q_T}] \tag{5.21}$$
关于这里的ENOB计算式:
应该和之前Data Converters中看到的表达式殊途同归,这个放到后面再推导吧~
注意到正弦拟合曲线方法没有给出有关误差的谐波失真相关内容。如果需要频率相关的性能测量,比如SFDR,THD等等,下一部分将讨论的FFT频谱分析技术是必须的。
需要注意的是,在今天,最常用的计算ENOB的方法利用了了信噪失真比,SINAD,本书第二章中有讲。SINAD可以简单通过FFT输出计算。然后就可以用下面这个式子,通过全量成SINAD计算出ENOB:
$$ENOB=\frac{SINAD-1.76dB}{6.02dB} \tag{5.22}$$
如果输入正弦波为满量程,相同情况下同一个ADC的测量结果应该近似一致。如果输入信号小于满量程,式5.22需要被纠正:
$$ENOB=\frac{SINAD-1.76dB+Level,of,Signal,Below,FS}{6.02dB} \tag{5.23}$$
FFT基础
这一部分关注于FFT的理论知识,而不是数学。
注意:
由于本人有一定的DSP基础知识,这部分简略地看,仅在本文中翻译记录一些重要的点。
FFT是数字信号处理的基础。图5.50给出了DFT在数字信号处理中的应用:
图5.51给出了傅里叶变换大家族。这其实就是根据是否周期、是否连续,把傅里叶变化分为四象限。信号课中反复提及,这里不再赘述。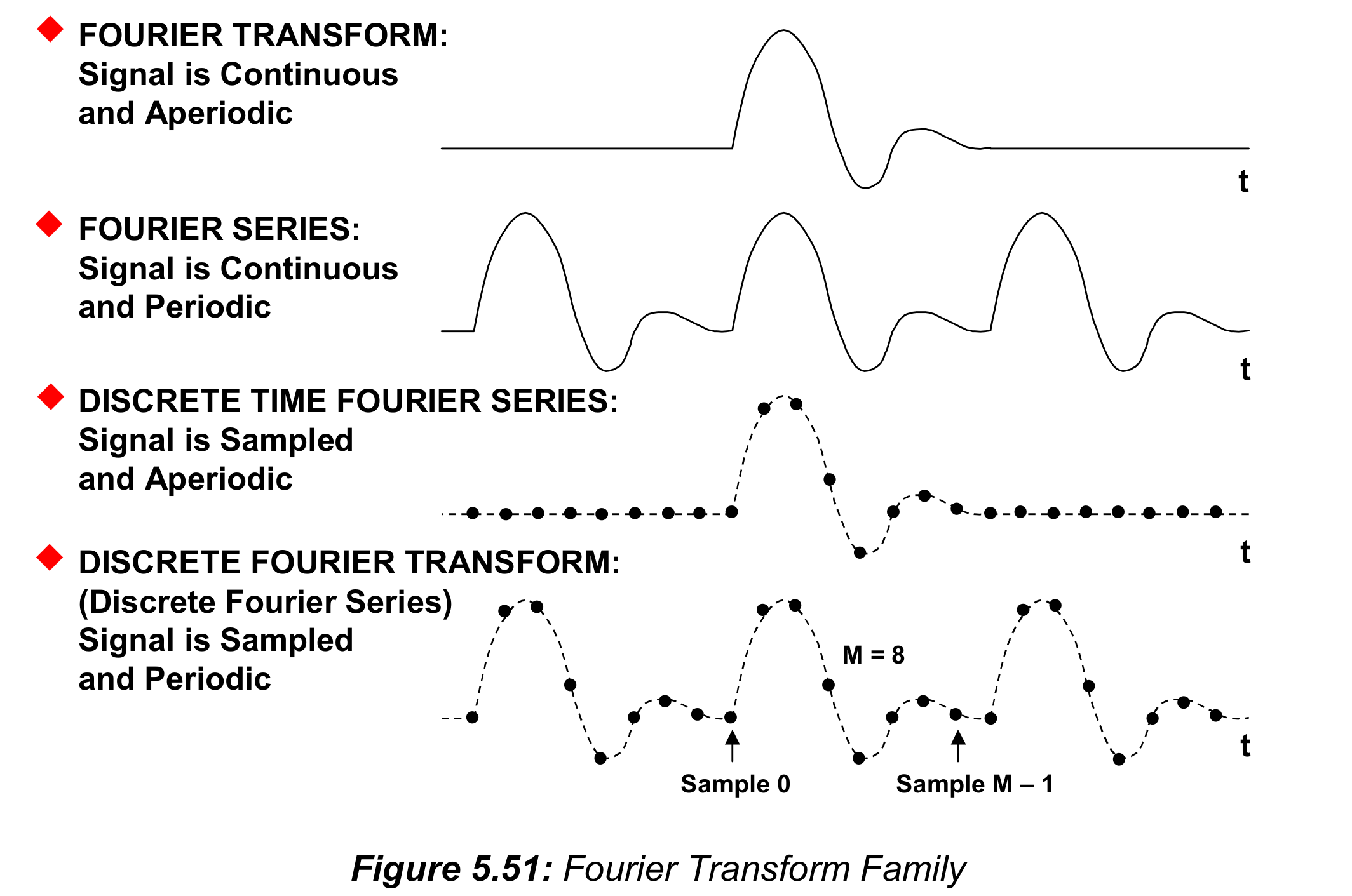
图5.54展示了Processing Gain的影响: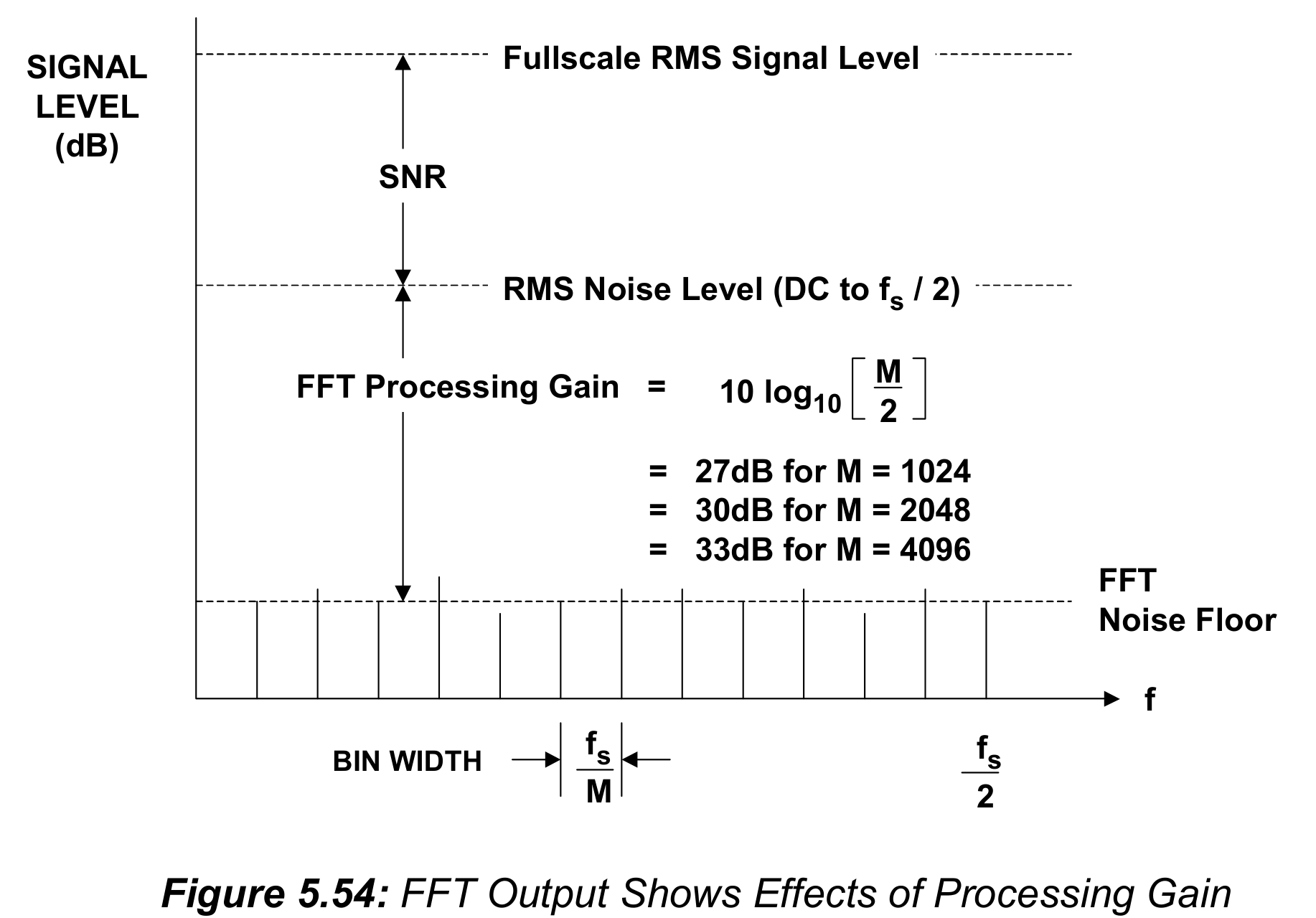
需要注意的是,如果为了减小缓存压力,把它的时钟调为$f_s/K$的话,从FFT的角度来看,采样频率就是$f_s/K$。需要信号频率不要大于$f_s/2K$,否则会有频谱混叠。
为了得到纯净的频谱,而不发生频谱泄露,记录的数据必须包含整数个周期,这样产出的频谱就只有单根谱线。通过单频正弦波的FFT最能够理解频谱泄露。
FFT测试装置配置和测量
图5.62展示的典型的FFT测试装置,可以通过多种方式实现。最大限度地利用生产商提供的评估板能够大大简化测试,并且确保ADC周围关键元件的恰当布局。一个设计优良的评估板应该有输入缓冲放大器和/或变压器来驱动ADC,有采样时钟调理电路(或许甚至是稳定的晶振),电压参考(如果需要),输出数据寄存器,以及适当的输入输出连接器。这时再怎么强调低抖动采样是中原的重要性都不为过(The importance of … cannot be overemphasized at this point)。在之前第二章中已经讨论了采样时钟抖动对ADC SNR的影响,本书的第六章会对低抖动时钟源有进一步的建议。仔细注意接地、布局和去耦也很重要,因为将数字输出耦合到时钟或ADC中会降低SNR,SINAD和SFDR表现。出于这些原因,强烈建议使用制造商的评估板。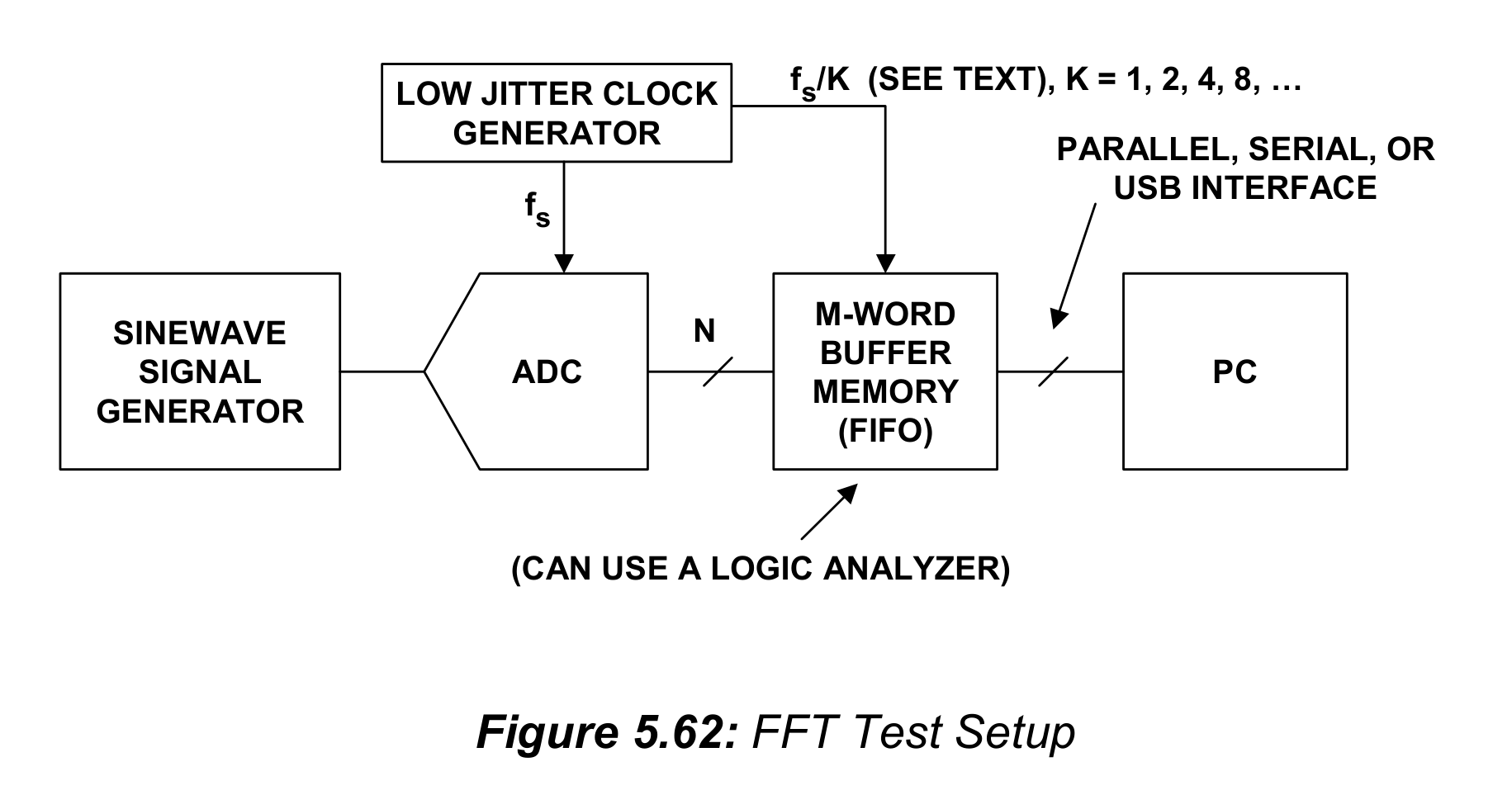
需要指出的是,在今天,有大量常用的商用软件包会包含FFT,因此没必要去亲自写FFT软件。
为了进一步简化评估过程,ADI提供了高速ADC FIFO评估工具,能够直接连接到评估板上的连接器(见图5.63).FIFO评估工具包含用来从ADC捕捉数据块的内存板,以及Windows兼容的ADC分析软件。FIFO板能够通过标准打印线缆连接到PC的并行接口,并且与ADC分析软件一起使用来快速评估高速ADC性能。
FIFO板包含两个32K,16-bit宽的FIFO,每个通道上的数据能够以最高133MSPS的速度被捕捉。内存可以升级,将FIFO提升到64K,132K或者256K。FIFO有两个可用版本:一个是给双通道或者多路解码数字输出的ADC使用的,另一个给单通道的ADC使用。用户可以观察FFT输出并且分析SNR,SINAD,SFDR,THD,以及谐波失真信息。
在ADC分析软件计算FFT后,有两个方法来评估ADC表现:图形或者计算。为了更有意义地展示数据,幅度数据需要转换为分贝(dB)。可以使用这个式子来完成:
$$dB=10log_{10}[\frac{Mag^2}{Mag_{Max}^2}]=20log_{10}[\frac{Mag}{Mag_{Max}}] \tag{5.28}$$
其中Mag是幅度,在这里就是FFT计算结果中的元素。
使用评估板和分析软件绘制的FFT图如图5.64中所示,使用AD9430,12-bit,170-/210-MSPS ADC。对这个测试,采样频率是170MSPS,输入频率是10.314MHz,FFT大小是M=16384($2^{14}=16384$)。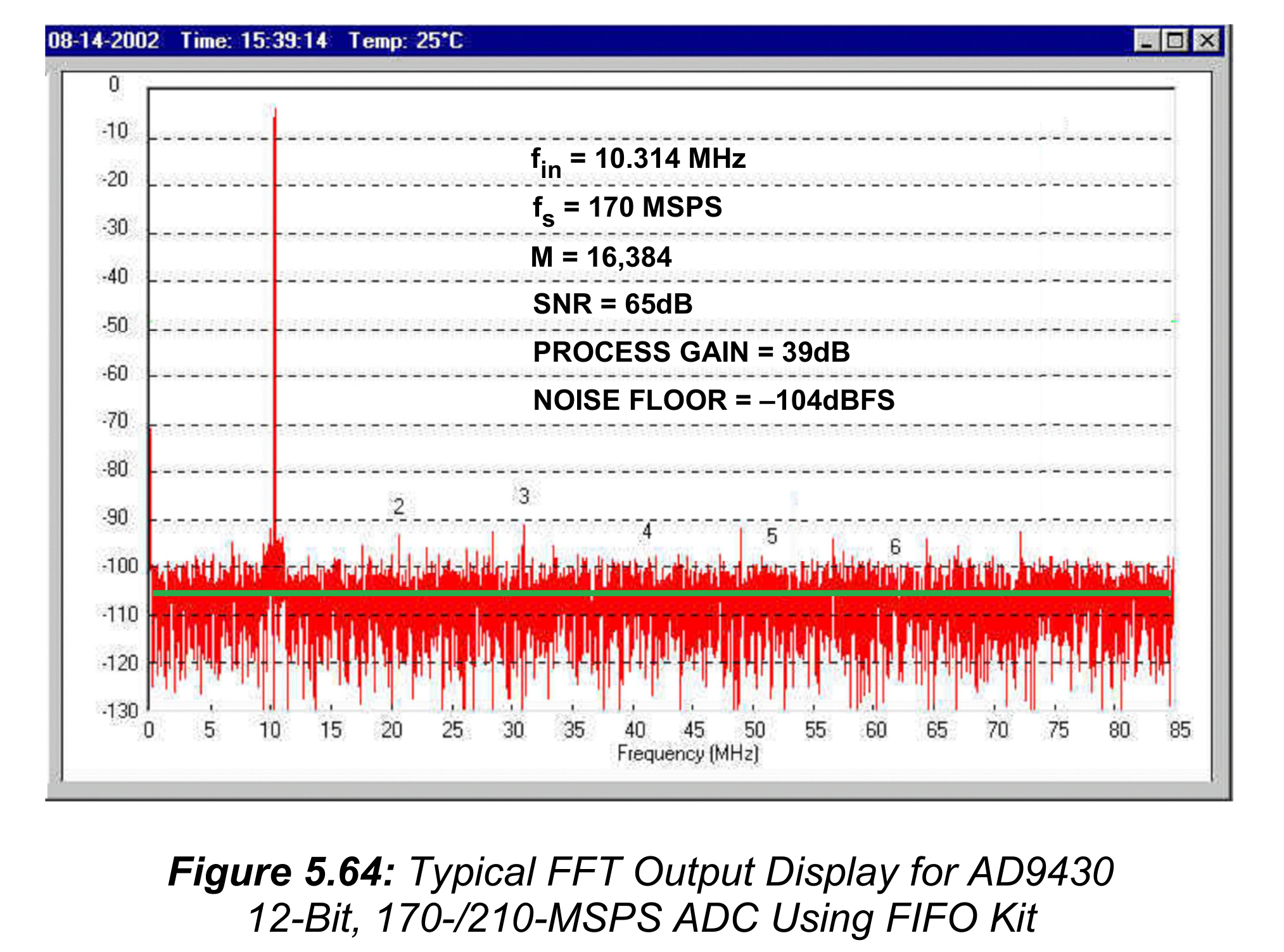
ADC分析仪软件配置文件的关键输入在图5.65中展示。注意,对几次FFT求平均得到的结果并不会改变FFT噪底(noise floor),知识减少了随机噪声的变化。文件的大部分输入是不言自明(self-explanatory)的,但是相干与非相干采样的问题值得进一步讨论。
如果使用了相干采样,基频和谐波分别都会落在一个谱线里,像图5.66中展示的那样。输入频率$f_{in}$与采样频率$f_s$之间的严格关系遵循:
$$\frac{f_{in}}{f_s}=\frac{M_C}{M} \tag{5.29}$$
这其中$M_C$是全部记录的数据包含的输入正弦波的整数周期数。在进行SINAD计算时,除了直流分量意以外,所有频点上的和方根(rss,root-sum square,平方-求和-开根号,与均方根rms的区别是求和后不用均值)值就是噪声和失真能量的值。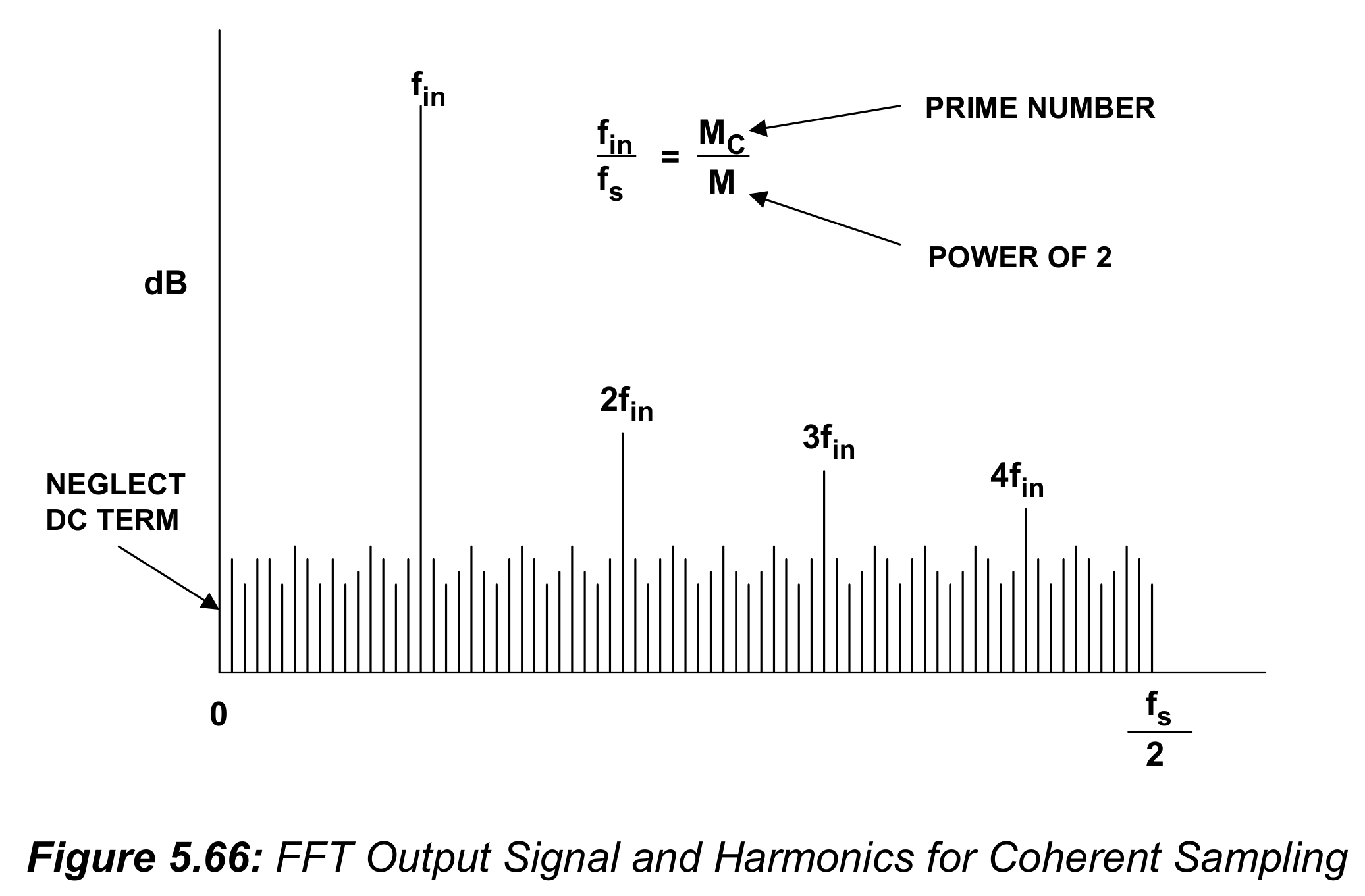
为了防止数据记录中图案重复,并且保证随机的量化噪声,$M_C$必须是一个素数。
关于素数:
后面的问题有关于这个的讨论。如果采样数据本身是周期重复的,那么量化噪声就是周期重复的,使得量化噪声失去了随机性,这是不好的;但是如果不使用素数,会不会出现高次谐波?后面再讨论吧。
为了保持确定的关系,输入频率和采样频率应该使用锁定频率合成器生成。ADC分析软件包含一个相干采样计算器,来实现输入频率的计算。为了使用相干频率计算器,必须在配置文件中输入正确的采样频率。然后近似的模拟输入频率和正弦波周期数也要输入。接着,计算器会根据输入的值推荐一个相干输入频率以及周期数。
如果使用了非相干采样,基频和谐波的能量就会泄露进相邻(adjacent)的频点,如图5.67中所示。如同之前讨论的那样,泄露的数量取决于实际使用的窗函数。当计算基频和谐波的能量时,应当像图5.67中一样使用相邻频点的和方根(rss)值。很重要的一点是,不要把相邻的这些点当作噪声频点,这会给出一个不准确的SNR计算。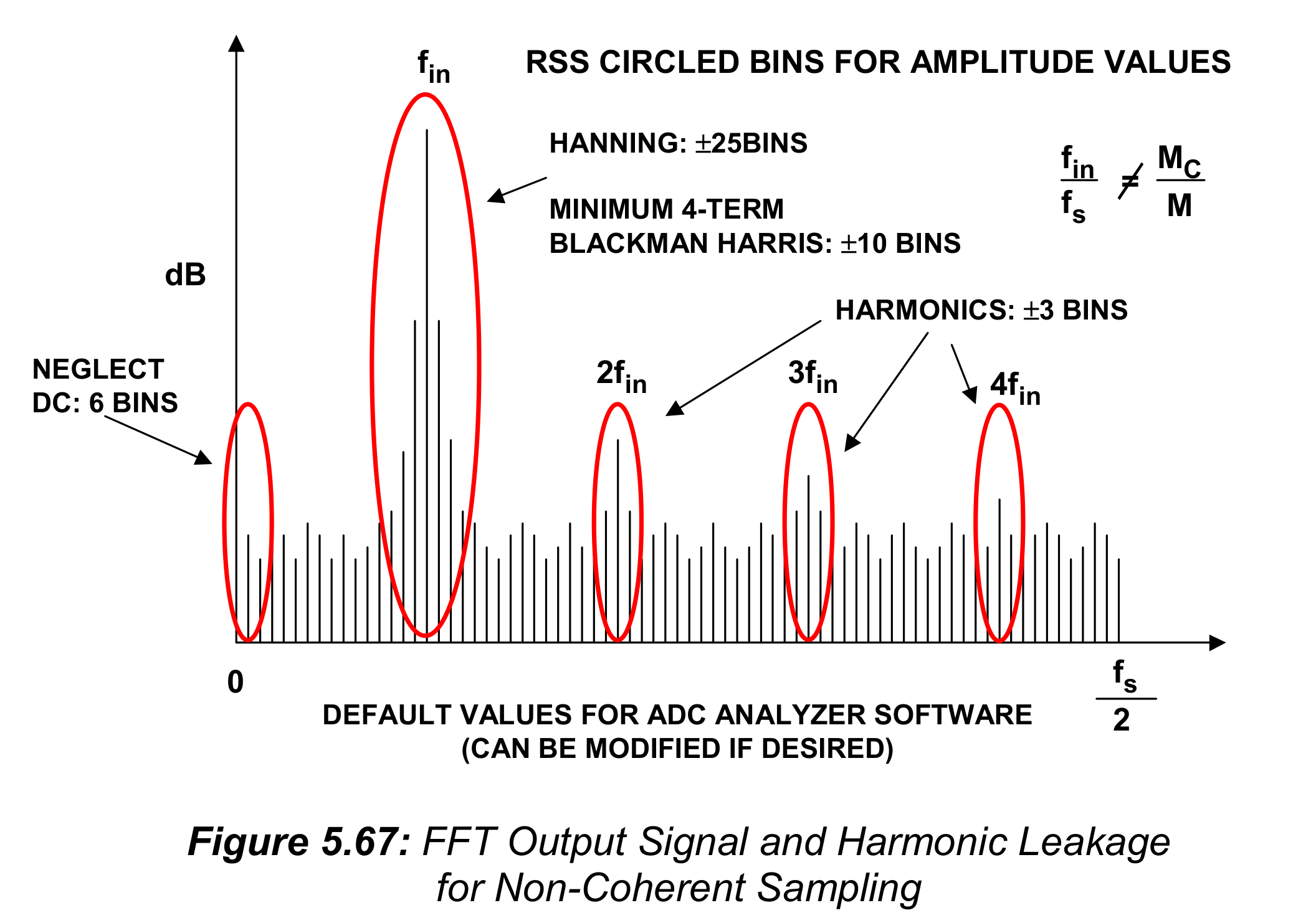
使用非相干采样时,FFT输出的直流分量也会出现泄露,这些点也应该从噪声计算中排除掉,防止错误的(erroneous)结果。在ADC分析软件中给出了默认的泄露频点数,对Minimum 4-term Blackman-Harries窗而言是$\pm 10$个频点,而对Hanning窗而言是$\pm2 5$个频点。谐波泄露的默认值是$\pm 3$个频点,直流泄露的默认值是6个频点。如果需要的话,这些泄露的默认值都可以修改,尽管默认值能在大部分情况下工作地很好。
如果考虑信号的泄露,SNR和SINAD的测量会被极度(drastically)影响。用于计算SNR的噪声的值是通过计算所有噪声点的rss值获得的,不考虑直流、基频以及2-6次谐波处的泄露。因此,考虑幅度高于噪底的信号或者直流泄露点将会给出一个低于实际的SINAD测量值。
SINAD计算中,噪声和失真的值是通过计算所有噪声和失真的rss值来获得的,不考虑泄露点。因此,将幅度高于噪底的信号、谐波和直流泄露点考虑进来,给出的SNR会低于实际的值。
关于SNR的说明:
加窗之后尽管信号对应的bin多了,但是功率会减小。不要想当然的以为。写了个matlab程序检验,确实如此,信噪比会减小。
使用相干或者非相干测试很大程度上是偏好问题。尽管相干测试会除去对加窗的需求,选择恰当的频率以及它们的比值会变得冗长,尤其是当需要进行多频测试的时候。有人认为相干测试更适合于实验室环境,而非相干测试更像真实世界中的应用,其中确切的输入频率是未知的。在实际应用中,只要实验正确进行,两种方法都能得到近似相同的最终结果。
ADC分析软件不仅给出FFT图,也会计算许多性能特性,其中单频测试的特性总结在了图5.68中,双频测试的特性总结在了图5.69中。

验证FFT准确性
在许多情况下,需要对FFT软件做某种类型的测试验证,独立于待测的实际ADC。这个测试能以很多种方式完成。一个简单的方法是,禁用几位ADC LSB然后看SNR与SINAD的计算值是否接近减少后分辨率的理论值。这里的假设是高性能12-或14-bit ADC应该能接近8-bit水平的理论性能。LSB可以在软件或者硬件中禁用。
另一个方法需要生成理想的N-bit数字正弦波,通过FFT运行数据,然后将结果与理论值比较。理想N位ADC的第n个样本可以写成:
$$v(n)=INT[2^{N-1}sin(\frac{2\pi nf_{in}}{f_s})] \tag{5.30}$$
这里INT函数是简单地阶段了小数部分。
通过FFT获得的SINAD和SNR能与理论值进行比较,而且FFT历程的动态范围可以通过简单地增加N来找到,直到SINAD和SNR不在随着每位分辨率的增加而增长6.02dB。
生成低失真正弦输入
生成用来进行低失真高频测试的频谱纯净的测试信号,是一项有挑战性的任务。尽管有低失真信号发生器可用,但它们很昂贵。如果做快速评估时没有这些仪器,恰如其分的滤波也能从低成本发生器中产出合适的测试信号。
生成单频低失真信号的一个测试装置如图5.70所示: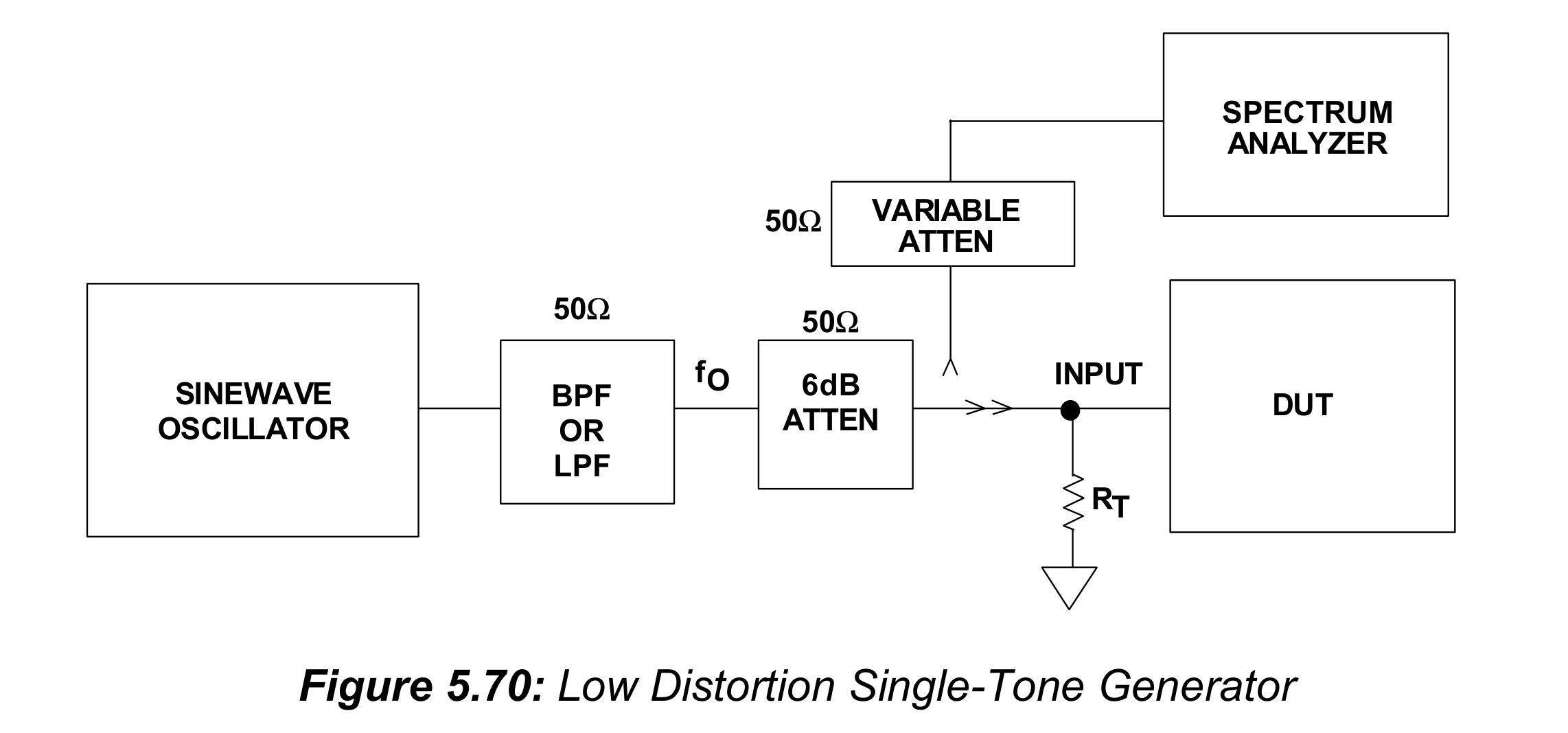
正弦波振荡器应该有低相位噪声,来防止ADC噪底的升高(elevation)。振荡器的输出要通过一个带通(或者低通)滤波器,它能移除振荡器输出中出现的任意谐波.如果发生器本身的失真足够低,也许就不需要滤波器了。发生器的失真得比测量需要的精度低10dB。一个6-dB衰减器将待测设备(Device Under Test),也就是ADC,与滤波器输出隔离开来。每个接口处的在抗都应该保持在60欧来得到最佳性能(也可以使用75欧原件,但是50欧衰减器和滤波器更容易获取)。选择终端电阻,$R_T$,使得它与待测设备的输入阻抗的并联值是50欧。
为进行IMD测试生成双频信号也很有挑战性。图5.71展示了一个低失真双频信号发生器: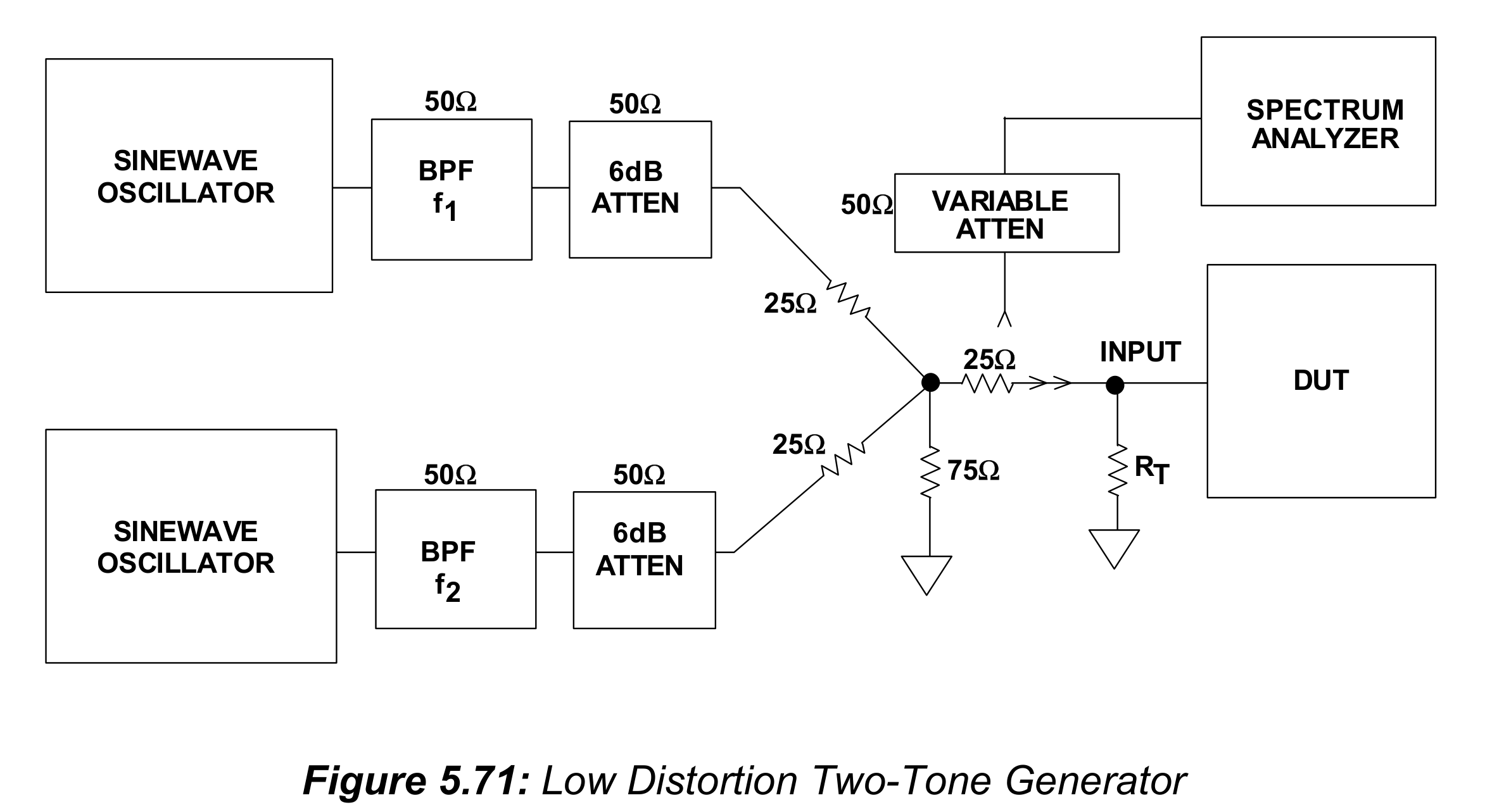
如图所示,需要两个带通(或低通)滤波器。每个滤波器的谐波抑制必须比需要的精度高至少6dB。每个滤波器输出端的6dB衰减器充当将输出互相隔离并防止可能的交调的角色。衰减器的输出组合在无源的50欧网络中,这个组合网络驱动待测设备。振荡器的输出设置为需要的电平,然后测得最终输出的IMD。测量应该使用单个端接电阻,并再次连接待测设备来识别非线性负载。
关于电阻网络:
衰减器的输出电阻是50欧,与25欧电阻串联得到75欧。三个75欧电阻并联得到25欧电阻,再与25欧电阻串联得到输出电阻为50欧。
测量这类信号时,模拟频谱分析仪需要独立地检查失真。大部分具有50欧输入电阻,因此待测设备和分析仪之间需要一个隔离电阻来仿真50欧以上的负载。在调整了频谱分析仪的带宽、扫描速度和灵敏度后,仔细检查输入过驱动,如图5.72中展示的那样: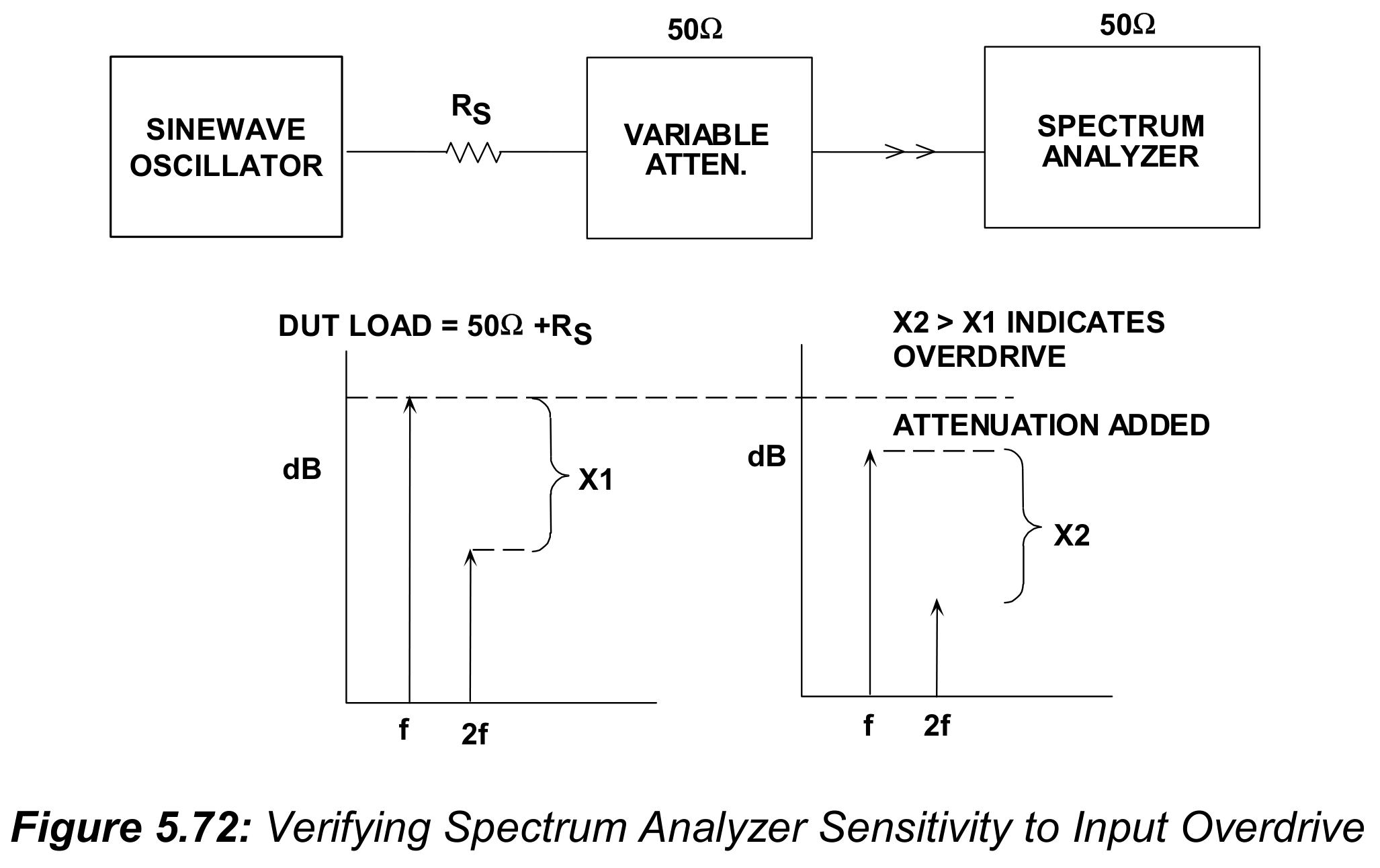
最简单的方法是:在分析仪输入路径上,使用可变衰减器来引入定量的衰减。信号和任意谐波都应该按照频谱分析仪上显示的以相同的定量衰减(例如10dB)。如果谐波衰减超过10dB,那么分析仪的输入放大器就引入了失真,灵敏度就会降低。许多分析仪在前面板上有衰减器来检查是否过驱动。需要指出的是,大部分高质量现代频谱分析仪,通常不像老的那些一样对输入过驱动那么敏感。但是,这些简单地检查不会花费太长时间,并且值得花费额外的努力来确保精准的失真测量。
如果发现发生器对过驱动很敏感,图5.73中展示了一个最小化此问题影响的方法。首先在关断陷波滤波器(notch filter)时测量基频信号。在打开陷波滤波器时测量谐波。陷波滤波器的插入损耗(insertion loss),X dB,必须加到测量的谐波电平中。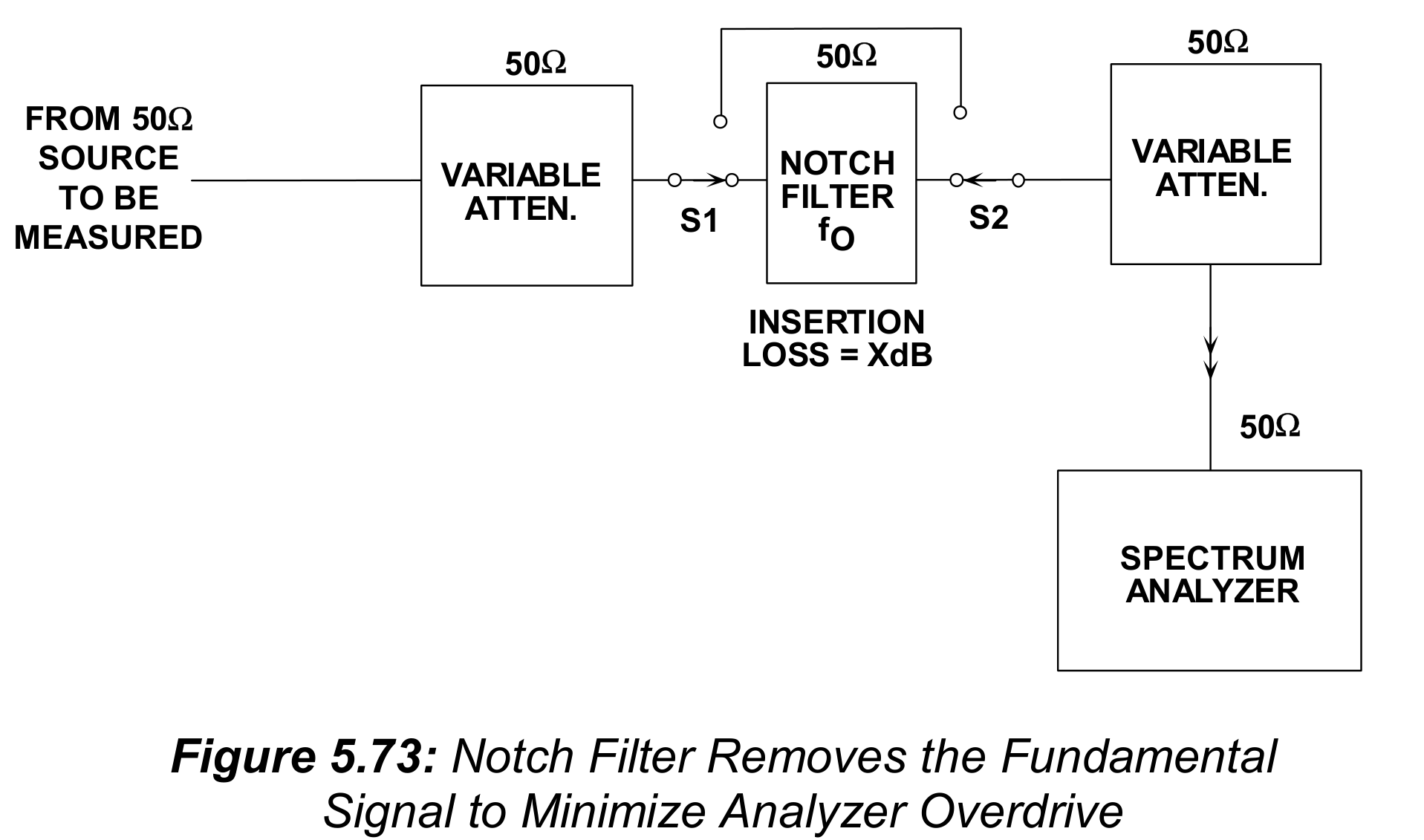
陷波滤波器:是一种带阻滤波器。
噪声功率比(Noise Power Ratio,NPR)测试
如同本书第二章中描述的,噪声功率比测量起源于频分复用(FDM)电话系统的早期。用高斯噪声仿真多路FDM信道,一个4kHz宽的信道从输入信号中“陷”出来。经过传输系统后,缺陷内的剩余信号代表了削波信号、热噪声和IMD失真的产物。简单地将缺陷外的平均噪声与缺陷内的平均噪声做比值就能得到NPR,也即,缺陷的“深度”。因为NPR是信号幅度的函数,输入信号幅度会变化,直到达到NPR的最大值。图5.74展示了测量ADC的NPR的简化测试装置。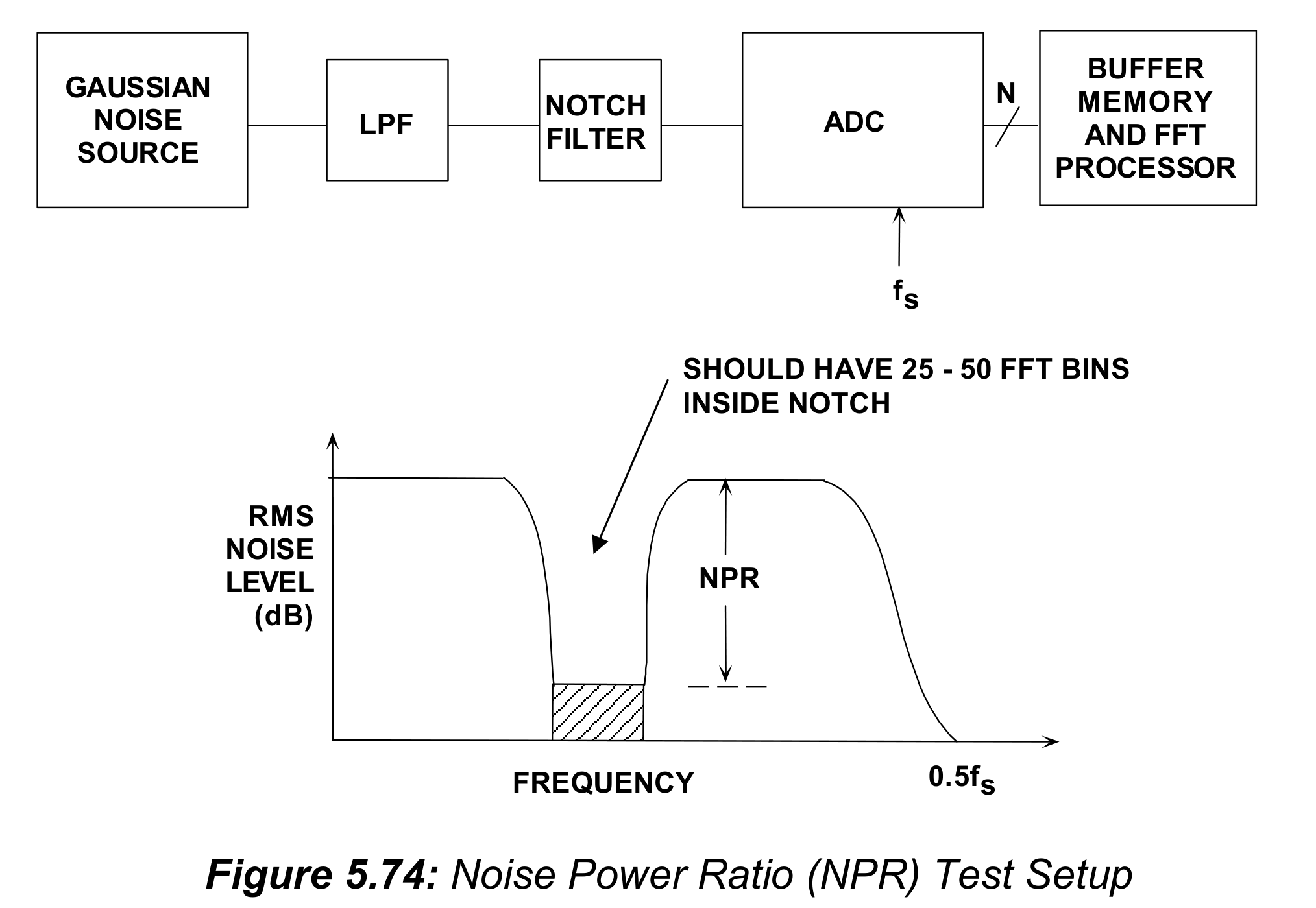
概念上讲,通过对ADC输出进行FFT并分析数据,可以简单地完成这个测试。但在实际中,为了测量4kHz宽的语音信道,需要相当大的缓存。例如,在170MSPS采样率下,一个256-K FFT的频率分辨率是170MSPS/256000=664Hz。这只能让4kHz的缺陷中包含6个频点–不足以获得噪声电平的可重复读数(图5.74中说到,缺陷需要包含25-50个频点)。解决方案是使用更宽的陷波滤波器,而不是使用不切实际(impractically)大的FFT。陷波滤波器宽度需要增加到使缺陷内包含至少25至50个样本。尽管使用了宽的缺陷,为了稳定NPR数据,需要对几次FFT进行平均。使用更宽的缺陷并不会以任何方式使结果无效,而会更接近的仿真现代通信系统中的更宽的信道。事实上,NPR测试是多频测试的很好的替代,假定输入频率不是相位相关的。在任何基于FFT的高性能ADC测试中,采样时钟抖动必须在可接受的低水平,以至于不会影响ADC噪底。
图5.75展示了一个典型的NPR,使用12-bit,170MSPS的 AD9430 ADC。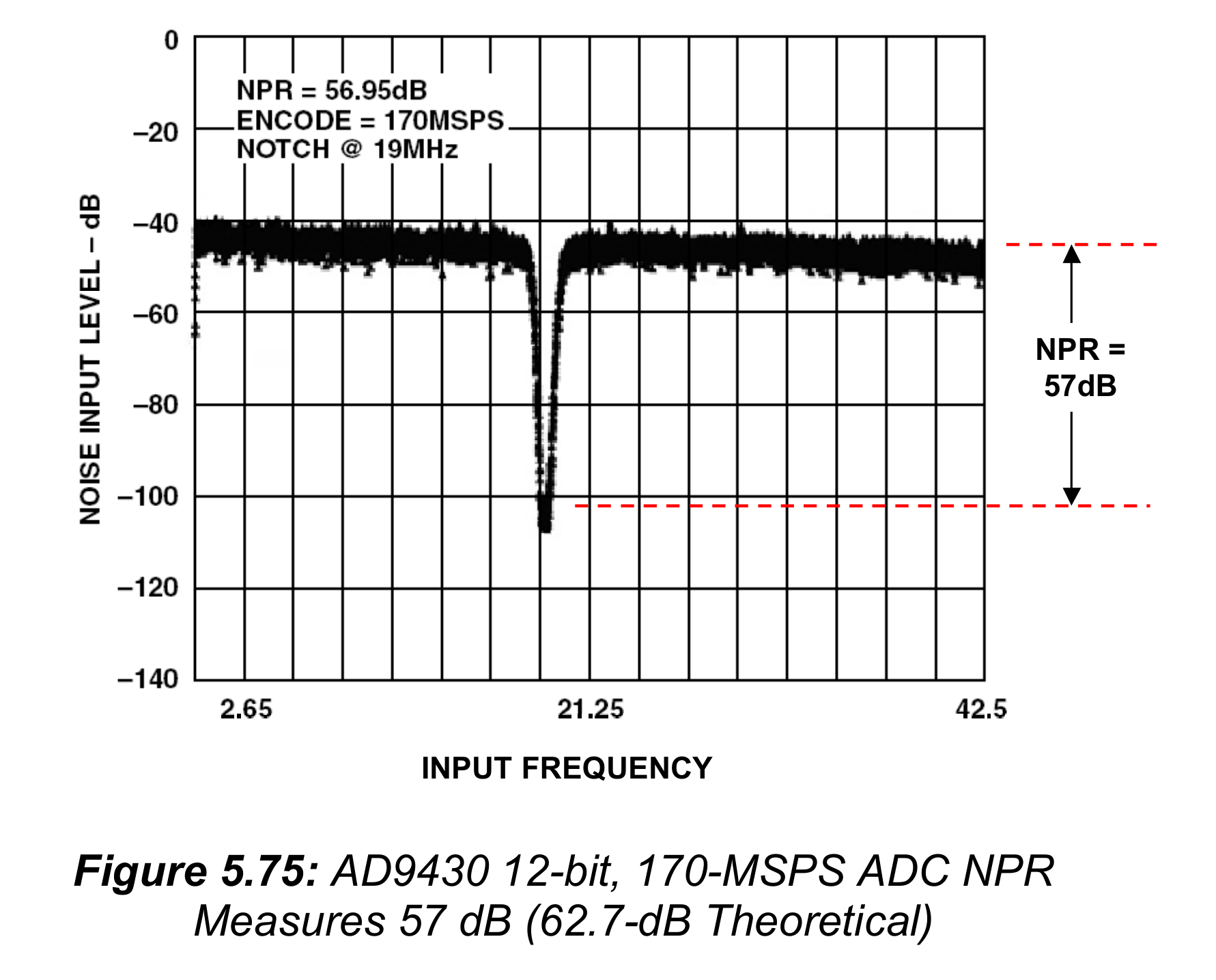
FFT大小是16384,使得频率分辨率是170MSPS/16384=10.4kHz。陷波滤波器宽度是大约500kHz,在缺陷中产生大约48个样本点。由于对中心频率,宽度和阻带抑制的特殊需求,为了在ADC上进行NPR测试,通常需要定制的陷波滤波器。
使用锁定直方图测试法测量ADC孔径抖动(Aperture Jitter)
定义:
在Data Converters中的定义如下:是采样时间的标准偏差。也称为孔径抖动和时间相位噪声。通常假定时钟抖动是白噪声。
图5.76展示了使用“直方图”测试来测量孔径抖动的测试装置。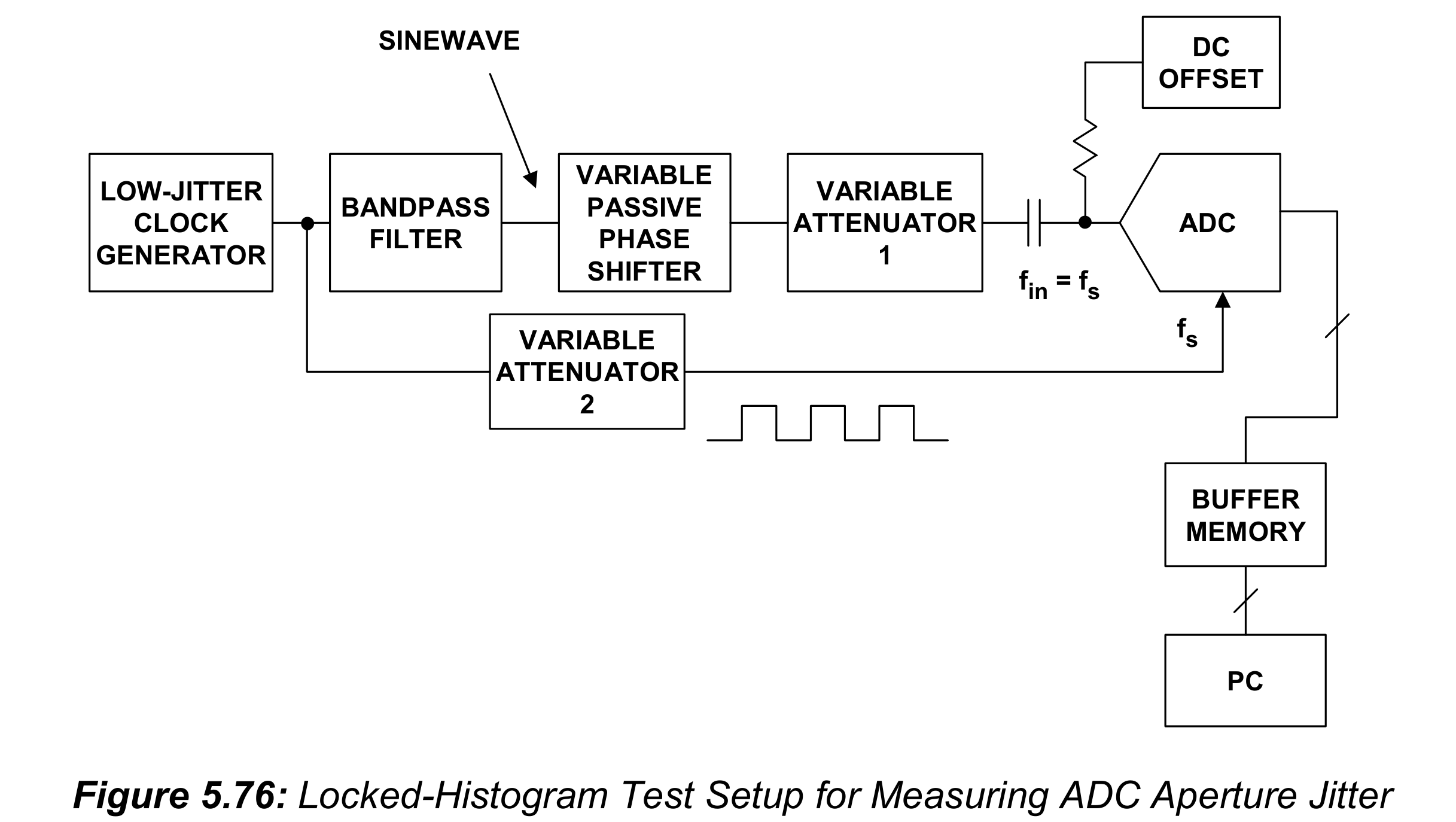
为了尽量减小两个信号之间的抖动,ADC输入信号和采样时钟来自于统一个低相噪时钟发生器。回想本书第二章中的讨论:采样时钟的抖动和ADC孔径抖动是无法区分的(indistinguishable)。理想情况下,此测试在ADC最大采样频率情况运行。但如果ADC输入带宽不够高,测试可以在最大采样频率的一半处运行。
时钟发生器通过一个衰减器直接驱动ADC的输入采样时钟。时钟发生器也驱动一个带通滤波器(来把方波转化为正弦波)。带通滤波器的输出通过一个无源的可变移相器,一个衰减器,然后交流耦合到ADC输入。通过把衰减器1调到最小衰减,然后调整时钟发生器的输出电平使得ADC输入信号是满量程的(峰峰值$2V_{FS}$),来校准装置。然后调整ADC的直流偏置,使得输入信号以量程中点为中心。然后,调节衰减器2来为ADC的输入采样时钟提供恰当的电平。
接着,增加衰减器1的衰减值,直到ADC的峰峰值输入只能经过量程中点上下的几个码字。调整可变移相器,使得大部分时间出现中量程代码。输入参考噪声可能会造成码字的分布–如果是这样,通过PC软件来计算分布的标准差,$\sigma_L$,以LSB为单位。这对应于用LSB表示的输入参考噪声。然后设置衰减器1使得ADC输入满量程。然后调节可变移相器,直到中量程码字有着最大的出现概率。新的码字分布的标准差,$\sigma_H$,现在包含了输入参考噪声以及孔径抖动。噪声源以rss为基础组合:
$$\sigma_H^2=\sigma_L^2+\sigma_A^2 \tag{5.31}$$
这里$\sigma_A$就是孔径抖动噪声的均方根值。
通过式5.31解出$\sigma_A$:
$$\sigma_A=\sqrt{\sigma_H^2-\sigma_L^2} \tag{5.32}$$
满量程输入正弦信号由式子:$v_{in}(t)=V_{FS}sin2\pi f_{in}t$ 给出,ADC的输入区间是 $\pm V_{FS}$ 。满量程正弦波在过零点处的变化率由下面这个式子给出:
$$\frac{dv}{dt}|{max}=V{FS}2\pi f_{in} \tag{5.33}$$
对于斜率 $dv/dt|{max}$ ,抖动时间$t_a$与对应的均方根电压误差$\Delta v{rms}$的关系式是:
$$t_a = \frac{\Delta v_{rms}}{\frac{dv}{dt}|{max}} \tag{5.34}$$
$\sigma_A$ 是以LSB为单位的均方根噪声,则对应的 $\Delta v{rms}$ 表示为:
$$\Delta v_{rms}=\sigma_A \cdot \frac{V_{FS}}{2^{N-1}} \tag{5.35}$$
把上面的式子带进去化简,得到:
$$t_a = \frac{\sqrt{\sigma_H^2-\sigma_L^2}}{2\pi f_{in}\cdot 2^{N-1}} \tag{5.36}$$
上述计算可以总结为图5.77: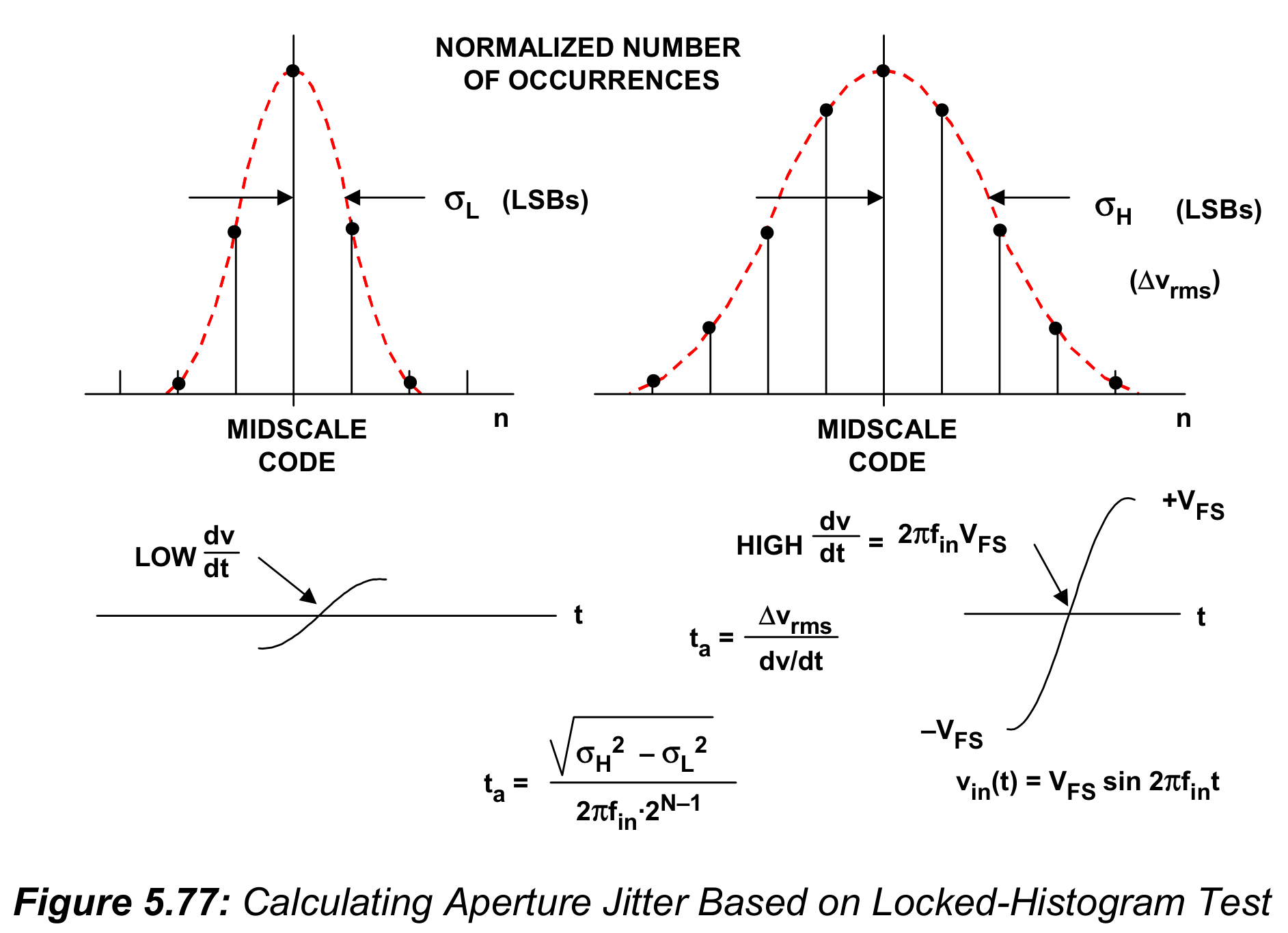
需要注意的是,测试装置可以使用低抖动正弦信号发生器来驱动ADC输入,然后使用同一个发生器的同步触发脉冲来驱动ADC的采样时钟输入。但是,如果孔径抖动的测量均方根值期望小于100ps,信号发生器输出和出发输出之间的抖动可能有相同的幅度,因此会破坏整体的测量。
测量孔径延迟时间
可以使用用来进行锁定直方图孔径抖动测试的同款测试装置来进行孔径延迟时间测试(图5.76中的),或者使用图5.78中更简单的测试装置。模拟输入频率被锁定到采样时钟的频率,加到ADC输入端的是满量程的正弦波。调整采样时钟的延迟,直到码字的PC直方图分布表明,ADC正在正弦波的过零点被采样,对应中量程码字。孔径延迟,简单来说,就是采样时钟的前沿(leading edge)的50%处点与正弦波的过零点的差值,使用双迹示波器测量。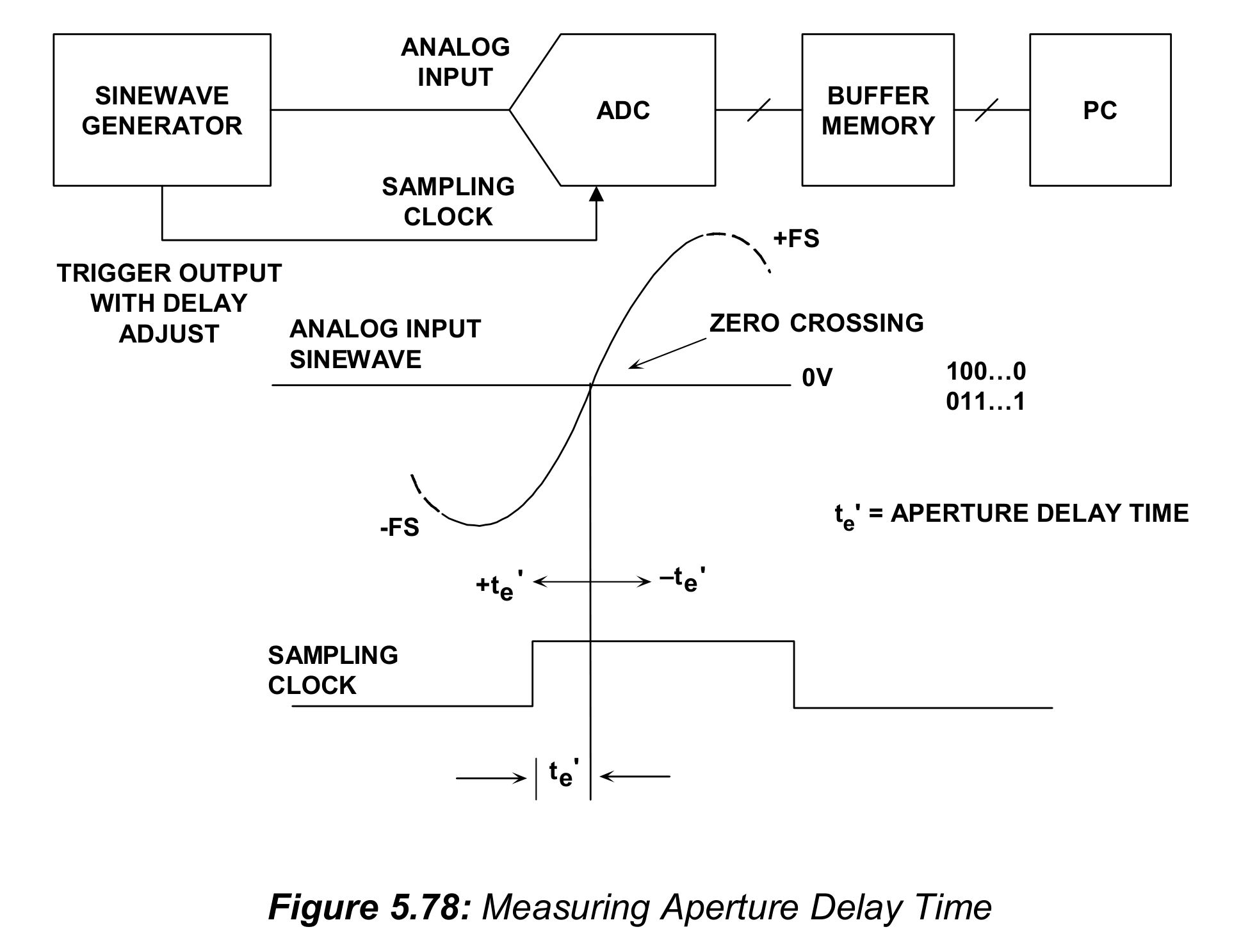
如图5.78中所示,孔径延迟可以是正的或者负的。正弦波输入信号的频率不是关键,但频率应该足够高,以至于可以精准地测量小的孔径延迟时间。但是,频率不应该超过ADC的模拟输入带宽。方便起见,ADC最大采样频率的一半是一个很好的起点,代表一个合理的上界。
使用FFT测量ADC孔径抖动
用于测量ADC SNR的FFT测量程序是能用来测量孔径抖动的极佳的非直接方法。这个测试中需要注意的是(The caveat in this test),本测试同时包含采样时钟发生器的抖动以及ADC内部的孔径抖动。因此,由于抖动是以rss形式结合的,需要挑选一个rms抖动规格比指定的待测ADC的孔径抖动小几倍的发生器。用于孔径抖动的基本测试装置,以及关键计算,都在5.79中展示出来了。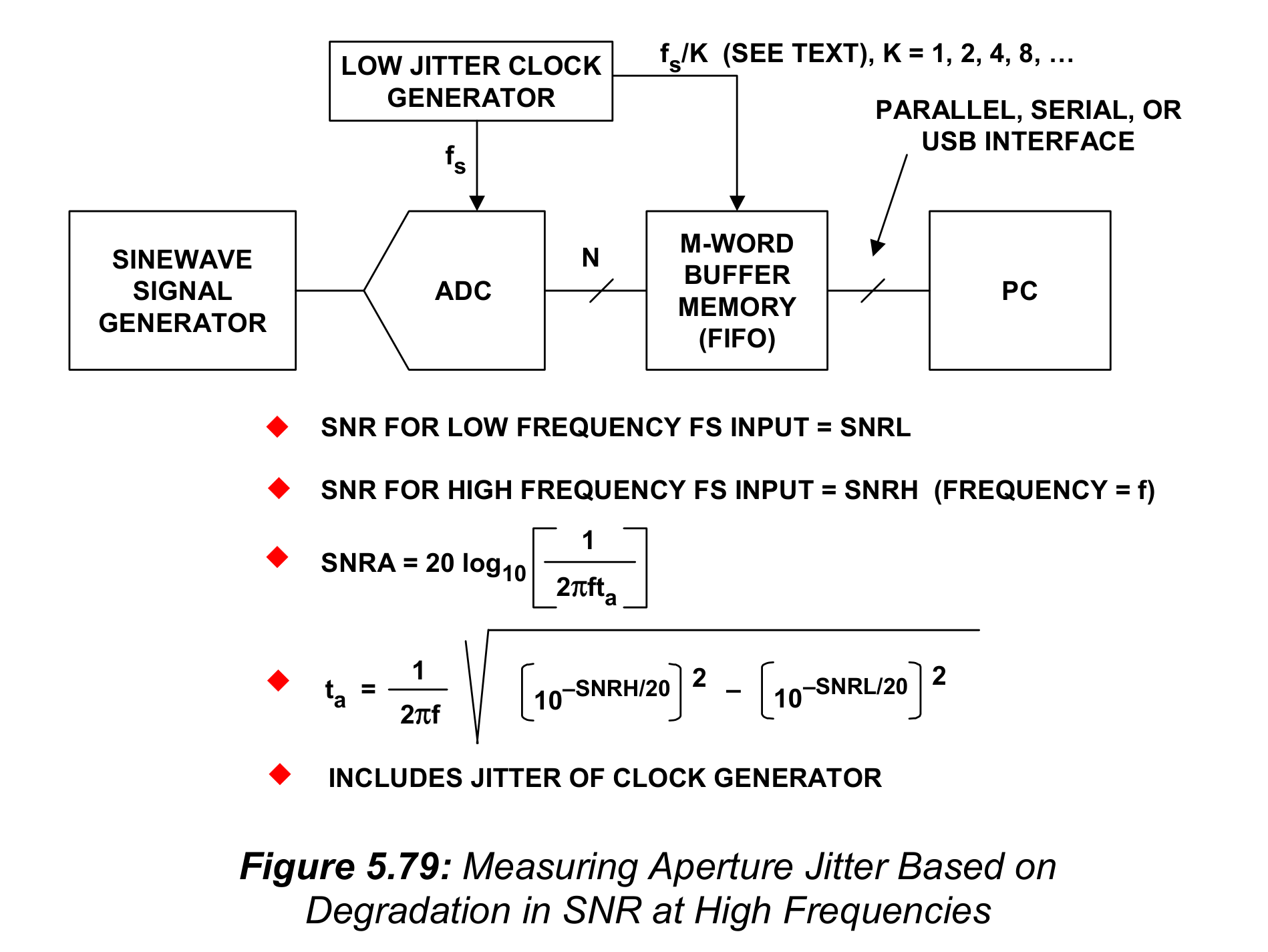
有两个SNR需要测量,它们都使用满量程正弦波输入。第一个测量是SNRL,在相对低频下进行,这时噪声主要是(primarily)ADC输入参考噪声。低输入频率改变很大(quite a bit),测得的SNR值依然是相同的。采样频率通常设定为允许的最大值。第二个测量,SNRH,是使用高频输入进行的,这时孔径抖动对ADC SNR的影响是很明显的(noticeable)。根据ADC的不同,这个频率可能能达到$f_s/2$。回想第二章中,孔径抖动单独导致的SNR由下面式子给出:
$$SNRA = 20log_{10}[\frac{1}{2\pi f t_a}] \tag{5.37}$$
关于式5.37:
这个式子在Data Converters中也给出了,1.2.2的式1.8,$SNR=-20log{<\delta_{ji}(t)>\omega_{in}}$,和式5.37是一样的。
回到正题。SNRA是孔径抖动导致的SNR(dB),f是输入频率。
整理式子,根据SNRA与SNRH,SNRL的关系,以及t与SNRA的关系,能够得到最终的抖动表达式:
$$t_a=\frac{1}{2\pi f}\cdot \sqrt{(\frac{1}{10^{SNRH/20}})^2-(\frac{1}{10^{SNRL/20}})^2} \tag{5.41}$$
需要强调的是,上面的测试需要的全部测量,都是SNR,而非SINAD。极其重要的一点是,在从FFT输出计算SNR的时候,2-6次谐波(以及直流分量)应该被移除。否则,将会无法给出孔径抖动的精准测量。
最后要注意的是(As a final note),测量均方根值小于10ps的孔径抖动是相当困难的,这仅仅是因为输入信号和采样时钟上可能会出现不想要的抖动,或者布局抖动和噪声。达到如此水平的精准需要极低抖动的频率合成器,以及注意布局,信号走线(signal routing),接地以及去耦。
使用FFT测量ADC模拟输入带宽
让输入频率从低频扫到高频,观察FFT输出显示,然后就能简单地测量出模拟输入带宽。频率增加的过程中,输入信号的幅度必须保持不变,并且观察FFT基频输出信号的相对幅度。当基频信号的幅度相对于一开始的幅度下降了3dB,这时的频率定义为3dB带宽。如果使用满量程输入信号,得到的就是满功率带宽(FPBW,full-power bandwidth),而如果使用低幅度信号得到的就是小信号带宽。注意到,这个FPBW的定义,没有对FPBW频率下FFT展示的失真的量做说明,这对一些ADC来说是相当大的(considerable)。
为了在测量带宽的时候把失真的影响考虑进来,有时我们会使用一个叫做有效分辨率带宽(ERB,effective resolution bandwidth)的规格,此规格定义的是满量程SINAD下降3dB时的输入频率,对应0.5位的ENOB损失。ERB可以通过上面描述的步骤测量,只是带宽的评判准则(criteria)变成了SINAD计算而不是基频信号幅度。
建立时间(Settling Time)
建立时间可以通过图5.80中的测试装置测量,该装置围绕一个平坦脉冲发生器,以及ADC的同步可调延迟时钟输入,展开(baesd around)。调整平坦脉冲发生器,给ADC一个略小于满量程的阶跃输入,同时调整时钟延迟使得输出落在最终值的1LSB以内。采样时钟前沿与输入脉冲的50%点 之间的延迟,可以通过双通道示波器测量。如果ADC输入参考噪声的峰峰值小于1LSB,可以使用简单的LED灯来观察ADC输出;而如果输入参考噪声的峰峰值大于1LSB,就需要使用直方图来确定最频繁出现的输出码字。采样频率不必要设定到最大值,可以按需减少。注意,孔径延时必须从测量得到的建立时间值中减去。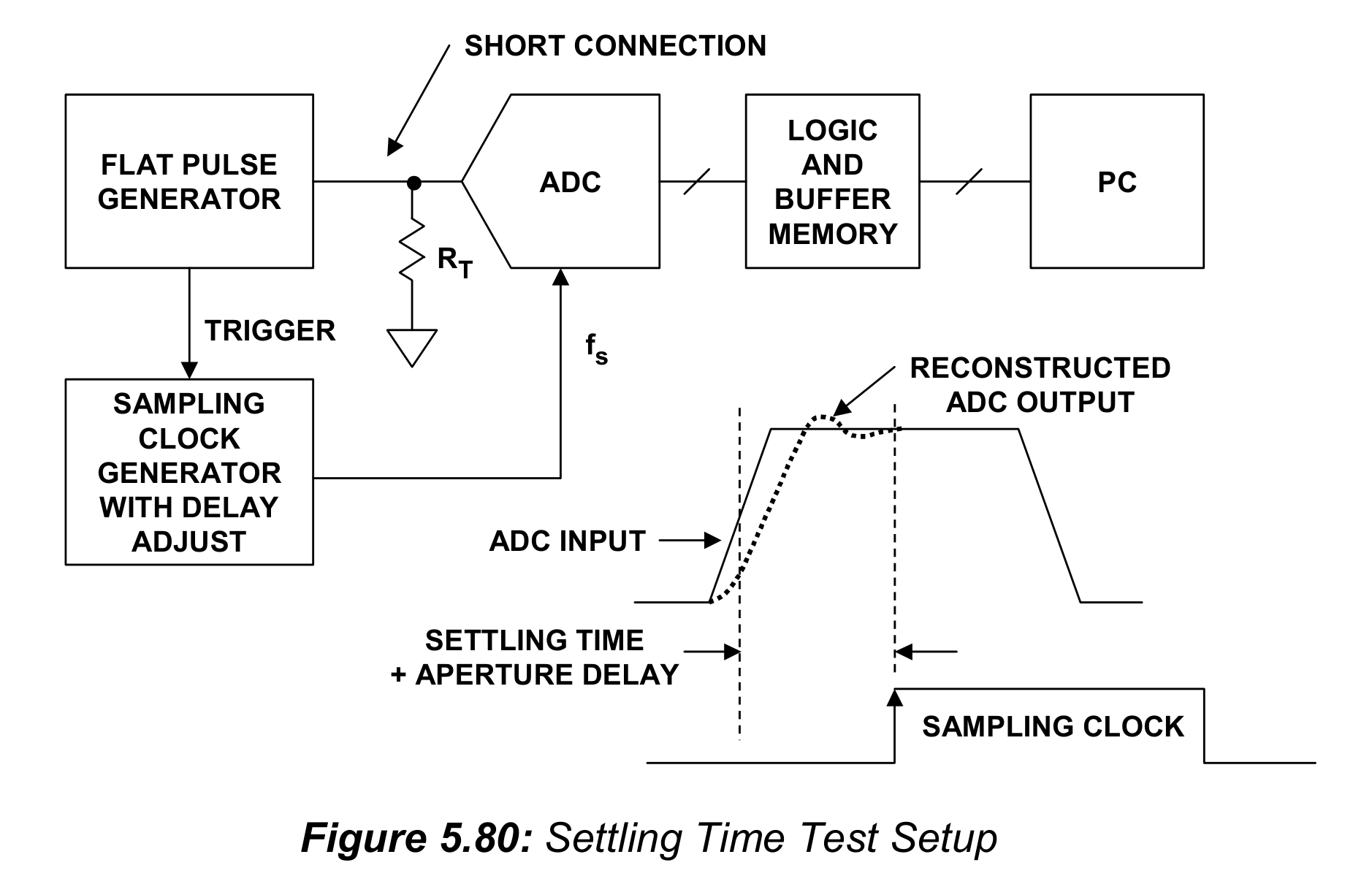
必须精确地直到平坦脉冲发生器的特性,其与ADC输出之间的距离必须最小。图5.81展示了一个简单的平坦脉冲发生器,以低电容肖特基二极管(Schottky diodes)为基础。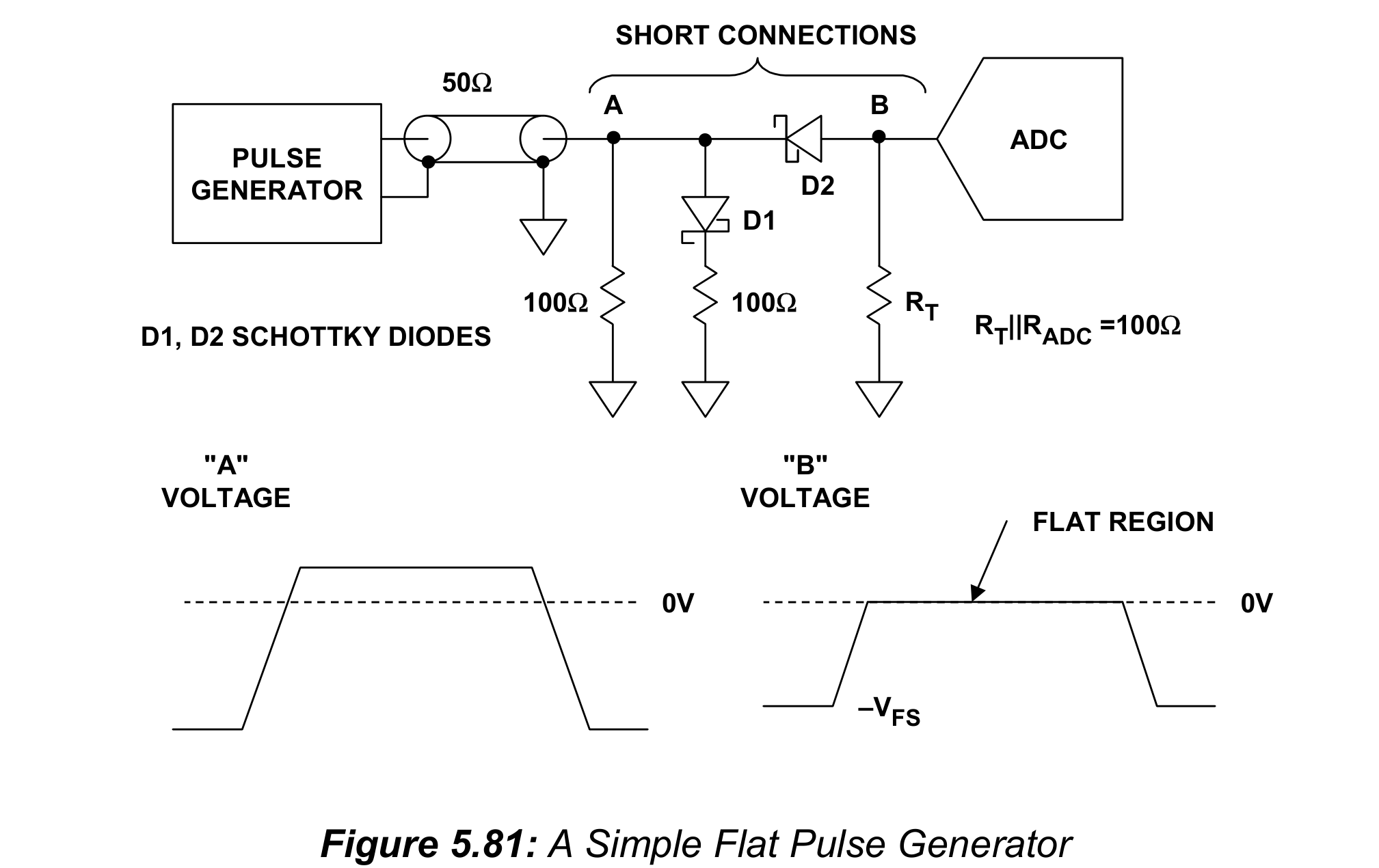
调整网络“A”的输出使得“B”处波形的起始点略高于ADC的负量程处。当“A”处电压变为正,D2管反向偏置,“B”处的电压是平坦的,除了由于反向偏置二极管电容导致的小的瞬态和刘瑾有效100欧电阻的小的反转漏电流。“A”处的电压不应该高于反向偏置D2所需电压。D1管确保当“A”是正的时候信号发生器端接在50欧的网络中。另一个管子可以与D2串联,来降低耦合电容,并根据需要调整“A”的负电压部分,来弥补额外管的电压降。如图所示,该网络能够向双极ADC提供1/2满量程脉冲。成功的关键是,把二极管-电阻网络与ADC输入连接地足够短和近。
过电压恢复时间
过电压恢复的测试装置与建立时间装置完全相同,只是“A”处电压需要调整,使得波形的起点在ADC范围外,如图5.82所示。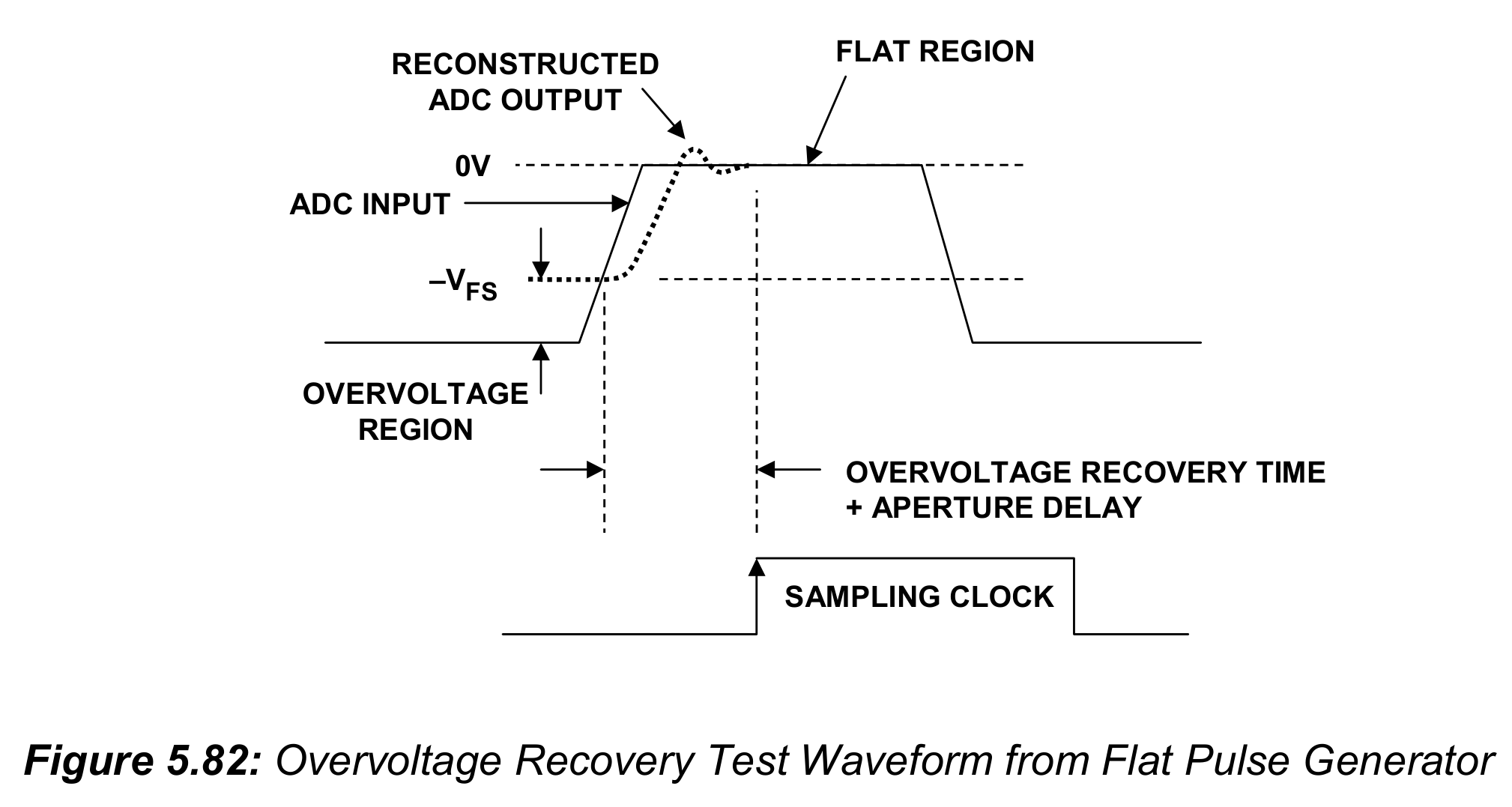
过电压量通常由ADC量程的百分比指定。对一个2V峰峰值的输入区间来说,50%过电压对应正常量程的1V以上或以下。
与瞬态响应测试一样,进行测试的时候必须考虑孔径延迟时间。
过电压恢复测试可以验证ADC在其标称范围外工作为理想限幅器。当输入信号在量程之外时,ADC会继续读为全“0”或全“1”.